Sección 7 R

7.1 Tipos de datos

Existen dos tipos de datos: atómicos y estructurados. Un dato atómico es aquel que se considera unidad mínima de información, como los números enteros y un dato estructurado es una colección de datos atómicos.

Datos atómicos:

Lógico: Datos que solo permiten los valores lógicos TRUE y FALSE.
Numérico: Datos cuyos valores son números reales.
Complejo: Datos cuyos valores son números complejos.
Caracter: Datos cuyos valores son cualquier tipo de carácter o cadena.

Datos estructurados:

Arreglos: colecciones multidimensionales de datos.
Vectores: Arreglos unidimensionales. Cada uno de sus elementos es del mismo tipo.
Matrices: Arreglos de dos dimensiones. Todos sus datos son del mismo tipo.
Dataframes: Son arreglos de dos dimensiones. Los datos de una misma columna son del mismo tipo pero puede variar el tipo de dato en diferente columna.
Listas: colecciones unidimensionales de datos donde cada elemento puede ser de un tipo diferente.

En R, casi todo lo que se manipula son objetos. Cada objeto tiene sus propias características como tamaño, dimensiones, longitud, tipo y sus propias funciones. Los objetos más comunes en R son:

Vectores
Matrices
Arreglos
Listas
Dataframes

7.1.1 Vectores en R

Uno de los objetos más simples pero poderosos de R son los vectores. Los vectores son listas ordenadas de datos. Para crear un vector usamos la asignación vector <- c("dato1", "dato2"). Por ejemplo, mi_vector <- c("hola", "clase", "1"), en este caso el elemento hola es el primer elemento del vector, además todos los elementos son del mismo tipo texto que llamaremos strings.

Podemos calcular la longitud de los vectores en R usando la función length(vector).

mi_vector <- c("hola", "clase", "1")
length(mi_vector)

## [1] 3

Los elementos de los vectores los podemos llamar a través de índices. R siempre indexa desde el número 1 a diferencia de Python que indexa en 0.

mi_vector[1]

## [1] "hola"

#Ejercicio: Crea un vector de números enteros

En R podemos realizar operaciones vectorizadas, es decir se pueden aplicar las operaciones a cada elemento de nuestro vector.

#Ejercicio: Realiza la multiplicación del vector que creaste por el número 2.

En R la mayoría de las operaciones matemáticas están vectorizadas como la multiplicación, raíces, divisiones, logaritmos o exponenciales.

c(2,4,6)/2

## [1] 1 2 3

c(1,2,3)^2

## [1] 1 4 9

Se pueden combinar también las operaciones vectorizadas e índices.

mi_vector2 <- c(2,4,6)
mi_vector2[2]*5

## [1] 20

Las sumas y restas tienen un comportamiento especial.

#Ejercicio: Crea dos vectores de la misma longitud y súmalos. 
#¿Qué realiza la suma de vectores? 
#¿Qué pasa si sumas vectores de diferente longitud?

Otras operaciones vectorizadas son las comparaciones. Los operadores de comparación que podemos usar en R son los siguientes:

== para ver igualdad.
!= para ver diferencia.
>= para ver si el lado izquierdo es mayor o igual que el derecho.
<= para ver si el lado izquierdo es menor o igual que el lado derecho.
> para ver si el lado izquierdo es mayor que el lado derecho.
< para ver si el lado izquierdo es menor que el lado derecho.

-1 <= 9

## [1] TRUE

c(1,2,3) == c(1,2,4)

## [1]  TRUE  TRUE FALSE

Si tenemos dos expresiones lógicas, podemos usar también los siguientes operadores:

& es la conjunción.
| es la disyunción.
! es la negación.

2 < 3 & 4> 1

## [1] TRUE

! 2 < 3

## [1] FALSE

Las sequencias regulares se pueden formar con el operador :.

x <- 1:3
x

## [1] 1 2 3

El operador : tiene prioridad sobre otros operadores.

#Ejercicio: ¿Qué obtenemos al realizar y <- 1:5-3?

Para formar una sequencia de números reales se usa la función seq, la sintaxis es como sigue: seq(from= 1, to=n, by=k, length.out = NULL ),

seq(from=1, to=40, by=5)

## [1]  1  6 11 16 21 26 31 36

seq(0, 1, by=0.1)

##  [1] 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0

#Ejercicio: ¿Qué pasa si invertimos el orden de las entradas en la función `seq`?
# seq(by=2, to=10, from=1)

La función seq se puede combianar con la creación de vectores.

x <- c(1, 2, 3, seq(4, 10, by=0.5))
#¿Cuál es la longitud del vector x?
#length(x)

Otra función que es útil para crear vectores es rep(Z,n), esta función crea un vector de n elementos todos iguales a Z.

y <- rep(2,10)
y

##  [1] 2 2 2 2 2 2 2 2 2 2

z <- c(x, y)
z

##  [1]  1.0  2.0  3.0  4.0  4.5  5.0  5.5  6.0  6.5  7.0  7.5  8.0  8.5  9.0  9.5
## [16] 10.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0  2.0

Las variables se pueden reescribir.

y <- c(y, "hola")
y

##  [1] "2"    "2"    "2"    "2"    "2"    "2"    "2"    "2"    "2"    "2"   
## [11] "hola"

#Ejercicio: ¿Qué sucedió con el vector y? 
#¿De que tipo son sus elementos ahora?
#Realizar la operación y+2.

Podemos convertir objetos de un tipo a otro compatible usando las funciones as.(nombre_del_nuevo_tipo_de_objeto). Por ejemplo, nuestro vector y ahora es del tipo caracter, podemos quitar el elemento que es de tipo caracter y convertirlo a un nuevo objeto ahora de tipo numérico.

y[11]

## [1] "hola"

w <- as.numeric(y[1:10])

as.numeric(TRUE)

## [1] 1

Las funciones elementales como exp, log, sin, etc las podemos aplicar a los vectores siempre y cuando los elementos de nuestro vector estén en el dominimo de la función correspondiente.

log(c(1,2,4))

## [1] 0.0000000 0.6931472 1.3862944

(Logaritmo<-log(c(-1,2,3)))

## [1]       NaN 0.6931472 1.0986123

Otras funciones útiles para vectores son:

max(x) y min(x): elemento máximo y mínimo del vector $x$.
sum(x) y prod(x): nos devuelve la suma y producto de los elementos del vector $x$.
mean(x) y var(x): nos devuelve la media y varianza del vector $x$.
sort(x): ordena los elementos del vector $x$ de manera creciente. Si agregamos el argumento decreasing=TRUE los ordena de mayor a menor.
order(x): nos da los índices correspondientes al ordenamiento de los elementos de $x$ de menor a mayor.

sort(c(6,2,9,10,4))

## [1]  2  4  6  9 10

order(c(6,2,9,10,4))

## [1] 2 5 1 3 4

sort(c(6,2,9,10,4), decreasing = TRUE)

## [1] 10  9  6  4  2

sum(c(6,2,9,10,4)); prod(c(6,2,9,10,4))

## [1] 31

## [1] 4320

mean(c(6,2,9,10,4)); var(c(6,2,9,10,4))

## [1] 6.2

## [1] 11.2

Podemos también seleccionar elementos de un vector y cambiarlos.

x <- seq(1,10,1)
x[c(2,4,6,8,10)] <- 0
x

##  [1] 1 0 3 0 5 0 7 0 9 0

x[c(3,5)]<-c(2,4)
x

##  [1] 1 0 2 0 4 0 7 0 9 0

En el caso de vectores de caracteres, dos funciones que son útiles son substr() y substring() las cuales nos sirven para extraer cierta cantidad de caracteres de cada entrada del vector. La sintaxis es la siguiente: substr(x,inicio,final) y substring(x,inicio,last=1000000L).

clases <- c("01.Matemáticas", "02.Español", "03.Ciencias", 
            "04.Física", "05.Geografía")
substring(clases,4,last=1000000L)

## [1] "Matemáticas" "Español"     "Ciencias"    "Física"      "Geografía"

substr(clases,1,2)

## [1] "01" "02" "03" "04" "05"

La función names() nos ayuda a darle un nombre a las entradas de los vectores, es decir en lugar de índices númericos ahora podemos asignarle un nombre a cada entrada.

mis_calificaciones <- c(10,8,9,7,8)
names(mis_calificaciones)

## NULL

names(mis_calificaciones) <- c("Matemáticas", "Español", "Ciencias", "Física", "Geografía")

names(mis_calificaciones)

## [1] "Matemáticas" "Español"     "Ciencias"    "Física"      "Geografía"

mis_calificaciones

## Matemáticas     Español    Ciencias      Física   Geografía 
##          10           8           9           7           8

7.1.2 Arreglos

Un array es una colección de datos, todos del mismo tipo, indexada por varios índices, es decir son objetos multidimensionales en R.

Si $dim=c(x_1,x_2,x_3...)$, donde $x_1$, $x_2$, $x_3$, etc son enteros, entonces $x_1$ es el número de filas, $x_2$ es el número de columnas, $x_3$ es el número de capas del array.

Una forma de crear arrays es primero crear un vector y después pasarle las dimensiones del arreglo.

x <- c(1:60)
# las dimensiones del array serán 6 filas y 10 columnas
dim(x) <- c(6,10)
dim(x)

## [1]  6 10

La función array() resume estas dos instrucciones. Su sintáxis es la siguiente: array(vector, dim = dimensiones).

# crea directo el array indicando vector y dimensiones
y <- array(c(1:60), dim = c(6,10))
y

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    1    7   13   19   25   31   37   43   49    55
## [2,]    2    8   14   20   26   32   38   44   50    56
## [3,]    3    9   15   21   27   33   39   45   51    57
## [4,]    4   10   16   22   28   34   40   46   52    58
## [5,]    5   11   17   23   29   35   41   47   53    59
## [6,]    6   12   18   24   30   36   42   48   54    60

La función class(objeto) nos permite conocer el tipo de objeto con el que estamos trabajando.

class(x)

## [1] "matrix" "array"

class(y)

## [1] "matrix" "array"

#Ejercicio: crear otro array z con el mismo vector x y 3 dimensiones y verifica el tipo de objeto que es z.

Las funciones ncol() y nrow() nos permiten conocer cuantas columnas y filas tienen los arrays en cada una de sus capas.

ncol(x)

## [1] 10

nrow(x)

## [1] 6

#ncol(z)
#nrow(z)

Como la función dim() nos dice las dimensiones de nuestro objeto, las funciones anteriores son equivalentes a lo siguiente:

# Número de filas
dim(z)[1]

## NULL

# Número de columnas
dim(z)[2]

## NULL

# Número de capas
dim(z)[3]

## NULL

Al igual que con los vectores, también podemos mandar a llamar las entradas del array indicando dentro de corchetes los índices. Si una dimensión se omite, R lo interpreta como que se piden todos los elementos de esa dimensión.

y[1,2]

## [1] 7

y[1,]

##  [1]  1  7 13 19 25 31 37 43 49 55

#Ejericio: Extrae la entrada (2,1,1) del arreglo z que creaste anteriormente.

Un array puede utilizar también otro array de índices, tanto para asignar un vector a una colección irregular de elementos de un array como para extraer una colección irregular de elementos.

indices <- array(c(1:6,1:6), dim=c(6,2))
indices

##      [,1] [,2]
## [1,]    1    1
## [2,]    2    2
## [3,]    3    3
## [4,]    4    4
## [5,]    5    5
## [6,]    6    6

# Asignamos el valor de 0 a las entradas dadas por el array indices
x[indices] <- 0
x

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    0    7   13   19   25   31   37   43   49    55
## [2,]    2    0   14   20   26   32   38   44   50    56
## [3,]    3    9    0   21   27   33   39   45   51    57
## [4,]    4   10   16    0   28   34   40   46   52    58
## [5,]    5   11   17   23    0   35   41   47   53    59
## [6,]    6   12   18   24   30    0   42   48   54    60

También podemos modificar manualmente las entradas del array de la siguiente forma.

x[5,7] <- 0; x[4,8]<- 0; x[3,9]<- 0; x[2,10] <- 0
x

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## [1,]    0    7   13   19   25   31   37   43   49    55
## [2,]    2    0   14   20   26   32   38   44   50     0
## [3,]    3    9    0   21   27   33   39   45    0    57
## [4,]    4   10   16    0   28   34   40    0   52    58
## [5,]    5   11   17   23    0   35    0   47   53    59
## [6,]    6   12   18   24   30    0   42   48   54    60

La función which() nos ayuda a recuperar los índices de un array que cumplan alguna condición. Su sintaxis es which(object, arr.ind = FALSE), donde object es el objeto de donde se quiere recuperar los índices y arr.ind se cambia a TRUE si se requieren los índices multidimensionales.

which(x<1, arr.ind = TRUE)

##       row col
##  [1,]   1   1
##  [2,]   2   2
##  [3,]   3   3
##  [4,]   4   4
##  [5,]   5   5
##  [6,]   6   6
##  [7,]   5   7
##  [8,]   4   8
##  [9,]   3   9
## [10,]   2  10

Está función también se puede aplicar a vectores.

(Logaritmo<-log(c(1,-2,3)))

## [1] 0.000000      NaN 1.098612

which(Logaritmo=="NaN")

## [1] 2

Las funciones y operaciones de los arrays son similares a las de los vectores.

# Sacar raíz cuadrada de la columna 1 del vector x
raiz_x <- sqrt(x[,1])
raiz_x

## [1] 0.000000 1.414214 1.732051 2.000000 2.236068 2.449490

#Ejercicio: Cambiar la columna 3 del array x por sus cuadrados.

La función dimnames es similar a la función names() de los vectores. En el caso de arrays, dimnames será una lista que debe contener tantos vectores como dimensiones tenga el array.

mi_array <- array(c(1:12), dim=c(2,2,3),
                  dimnames = list(c("Gato","Perro"),
                                  c("Esterilizado", "No esterilizado"),
                                  c("Morelia", "Patzcuaro", "Maravatio")))
mi_array

## , , Morelia
## 
##       Esterilizado No esterilizado
## Gato             1               3
## Perro            2               4
## 
## , , Patzcuaro
## 
##       Esterilizado No esterilizado
## Gato             5               7
## Perro            6               8
## 
## , , Maravatio
## 
##       Esterilizado No esterilizado
## Gato             9              11
## Perro           10              12

# Obtener la cantidad de gatos no esterilizados en Morelia
mi_array[1,"No esterilizado", "Morelia"]

## [1] 3

mi_array["Perro",,c("Morelia","Patzcuaro","Maravatio")]

##                 Morelia Patzcuaro Maravatio
## Esterilizado          2         6        10
## No esterilizado       4         8        12

#Ejercicio: Cambia el nombre de la ciudad Maravatio por alguna otra.

Las funciones rbind() y cbind() sirven para combinar arrays vertical y horizontalmente.

mi_array1 <- array(c(1:6), dim = c(2,3))
mi_array2 <- array(c(7:18), dim = c(4,3))
mi_array3 <- array(c(19:29), dim = c(2,5))

rbind(mi_array1, mi_array2)

##      [,1] [,2] [,3]
## [1,]    1    3    5
## [2,]    2    4    6
## [3,]    7   11   15
## [4,]    8   12   16
## [5,]    9   13   17
## [6,]   10   14   18

cbind(mi_array1, mi_array3)

##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,]    1    3    5   19   21   23   25   27
## [2,]    2    4    6   20   22   24   26   28

7.1.3 Matrices

Las matrices son arreglos de dos dimensiones. Entonces, una forma de crear una matriz es usando la función array pero especificando una dimensión de la forma dim=c(x,y).

matriz1 <- array(c(1:9), dim = c(3,3))
matriz1

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

Otra forma de crear matrices es usando la función matrix() indicandole el número de columnas y/o filas.

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

class(matriz1);class(matriz2)

## [1] "matrix" "array"

## [1] "matrix" "array"

matriz_ceros <- matrix(0, ncol=5, nrow=3)
matriz_ceros

##      [,1] [,2] [,3] [,4] [,5]
## [1,]    0    0    0    0    0
## [2,]    0    0    0    0    0
## [3,]    0    0    0    0    0

Otro parámetro que podemos darle a la función matrix es byrow, el cual nos ayuda a llenar la matrix por filas.

matriz3 <- matrix(c(1:9), nrow = 3, byrow = TRUE)
matriz3

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

Como las matrices son un tipo particular de los arreglos, las funciones como dimnames o extraer entradas y modificarlas funcionan de la misma forma.

#Ejercicio: Crea una matriz de tamaño 4x4 con números consecutivos ordenados 
#por filas y extrae la entrada (4,2).
#cambia los nombres de las filas y columnas por caracteres

Disponemos también de varias operaciones con matrices. La operación $A\ast B$ donde $A$, $B$ son matrices en R se refiere a la multiplicación entrada a entrada, no a la multiplicación de matrices. Además esta multiplicación solo se puede realizar si se tiene el mismo número de filas y de columnas.

matriz2 * matriz3

##      [,1] [,2] [,3]
## [1,]    1    8   21
## [2,]    8   25   48
## [3,]   21   48   81

La suma y resta de matrices se refiere a sumar o restar dos matrices entrada a entrada, solo se puede realizar con matrices de las mismas dimensiones.

# Suma
matriz2 + matriz3

##      [,1] [,2] [,3]
## [1,]    2    6   10
## [2,]    6   10   14
## [3,]   10   14   18

# Resta
matriz2 - matriz3

##      [,1] [,2] [,3]
## [1,]    0    2    4
## [2,]   -2    0    2
## [3,]   -4   -2    0

El operador en R para realizar la multiplicación usual de matrices es %*%.

matriz2 %*% matriz3

##      [,1] [,2] [,3]
## [1,]   66   78   90
## [2,]   78   93  108
## [3,]   90  108  126

El operador t() se usa para calcular la transpuesta de una matriz.

t(matriz1)

##      [,1] [,2] [,3]
## [1,]    1    2    3
## [2,]    4    5    6
## [3,]    7    8    9

7.1.3.1 Otras operaciones con Matrices

Crossproduct: es equivalente a t(A)%*% B o A %*% t(B). Las funciones que se usan son crossprod y tcrossprod respectivamente.

A <- matrix(c(10,8,5,12), ncol = 2, byrow = TRUE)
B <- matrix(c(5,3,15,6), ncol = 2, byrow = TRUE)

crossprod(A,B)

##      [,1] [,2]
## [1,]  125   60
## [2,]  220   96

tcrossprod(A,B)

##      [,1] [,2]
## [1,]   74  198
## [2,]   61  147

Producto exterior: El operador que se usa es %o% o la función outer().

A %o% B

## , , 1, 1
## 
##      [,1] [,2]
## [1,]   50   40
## [2,]   25   60
## 
## , , 2, 1
## 
##      [,1] [,2]
## [1,]  150  120
## [2,]   75  180
## 
## , , 1, 2
## 
##      [,1] [,2]
## [1,]   30   24
## [2,]   15   36
## 
## , , 2, 2
## 
##      [,1] [,2]
## [1,]   60   48
## [2,]   30   72

outer(A, B, FUN = "*")

## , , 1, 1
## 
##      [,1] [,2]
## [1,]   50   40
## [2,]   25   60
## 
## , , 2, 1
## 
##      [,1] [,2]
## [1,]  150  120
## [2,]   75  180
## 
## , , 1, 2
## 
##      [,1] [,2]
## [1,]   30   24
## [2,]   15   36
## 
## , , 2, 2
## 
##      [,1] [,2]
## [1,]   60   48
## [2,]   30   72

Producto Kronecker: si $A$ y $B$ son dos matrices, el producto de Kronecker se denota por $A B $ y en R el operador correspondiente es %x%.

A %x% B

##      [,1] [,2] [,3] [,4]
## [1,]   50   30   40   24
## [2,]  150   60  120   48
## [3,]   25   15   60   36
## [4,]   75   30  180   72

Potencia de una matriz: existen dos formas de realizarla. La primera es con el operador %^% del paquete expm. La segunda con la función matrix.power del paquete matrixcalc.

#install.packages("expm")
library(expm)

## Loading required package: Matrix

## 
## Attaching package: 'expm'

## The following object is masked from 'package:Matrix':
## 
##     expm

A %^% 2

##      [,1] [,2]
## [1,]  140  176
## [2,]  110  184

#install.packages("matrixcalc")
library(matrixcalc)
matrix.power(A,2)

##      [,1] [,2]
## [1,]  140  176
## [2,]  110  184

Determinante: la función de R que calcula el determinante de una matriz es det().

det(A)

## [1] 80

det(B)

## [1] -15

Inversa: para calcular la inversa de una matriz se usa la función solve().

solve(A)

##         [,1]   [,2]
## [1,]  0.1500 -0.100
## [2,] -0.0625  0.125

#Ejercicio: Verifica que efectivamente solve(A) es la inversa de la matriz A.

La función solve también nos ayuda a resolver un sistema de ecuaciones, por ejemplo si queremos resolver el sistema de ecuaciones $AX = B$ lo podemos hacer de la siguiente manera.

solve(A, B)

##         [,1]    [,2]
## [1,] -0.7500 -0.1500
## [2,]  1.5625  0.5625

Rango: no existe una función base de R para calcular el rango pero se puede usar la función qr() que nos calcula la descomposición QR de una matriz y regresa también como argumento el rango de la matriz o la función rankMatrix del paquete Matrix.

qr(A)

## $qr
##             [,1]       [,2]
## [1,] -11.1803399 -12.521981
## [2,]   0.4472136   7.155418
## 
## $rank
## [1] 2
## 
## $qraux
## [1] 1.894427 7.155418
## 
## $pivot
## [1] 1 2
## 
## attr(,"class")
## [1] "qr"

Para solo pedir a R el rango de la matriz se hace uso del operador $ de la siguiente manera.

qr(A)$rank

## [1] 2

library(Matrix)
rankMatrix(A)[1]

## [1] 2

Matriz diagonal: La función diag() nos ayuda a extraer o reemplazar la diagonal de una matriz.

#extraer la diagonal
diag(A)

## [1] 10 12

# reemplazar la diagonal
#diag(A) <- c(0,2)

Si el argumento que se le da a la función diag es un vector, esto crea una matriz diagonal con las entradas del vector en la diagonal.

diag(c(1,2,3))

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    2    0
## [3,]    0    0    3

Además, la función diag también nos permite crear una matriz identidad especificando solamente la dimensión de la matriz deseada.

diag(3)

##      [,1] [,2] [,3]
## [1,]    1    0    0
## [2,]    0    1    0
## [3,]    0    0    1

Eigenvalores y eigenvectores: la función de R que nos calcula tanto los eigenvalores como los eigenvectores es eigen().

eigen(A)

## eigen() decomposition
## $values
## [1] 17.403124  4.596876
## 
## $vectors
##            [,1]       [,2]
## [1,] -0.7339565 -0.8286986
## [2,] -0.6791964  0.5596952

#Para obtener solo los eigenvalores en orden decresiente 
#eigen(A)$values
#Para obtener solo los eigenvectores
#eigen(A)$vectors

7.1.4 Dataframes

Los dataframes o tablas de catos son un arreglo rectangular de datos y son los objetos más usados en R al momento de realizar análisis de datos. En los vectores, arreglos y matrices, todas las entradas tienen que ser el mismo tipo de dato pero en los dataframes no es necesario pero cada columna si debe de tener el mismo tipo de datos.

Para crear un dataframe usamos la función data.frame(), a diferencia de los arrays, uno debe especificar cada columna con su nombre. Los nombres de las columnas no deben de contener espacios.

mi_df <- data.frame(ciudad = c("Morelia", "Veracruz", "Merida"),
                    Temperatura = c(27, 26, 32),
                    Playa = c(FALSE, TRUE, FALSE))
mi_df

##     ciudad Temperatura Playa
## 1  Morelia          27 FALSE
## 2 Veracruz          26  TRUE
## 3   Merida          32 FALSE

Todas las columnas de un dataframe deben de tener la misma longitud. La función str()nos permite ver como están estructurados nuestros datos, no solamente un dataframe.

str(mi_df)

## 'data.frame':    3 obs. of  3 variables:
##  $ ciudad     : chr  "Morelia" "Veracruz" "Merida"
##  $ Temperatura: num  27 26 32
##  $ Playa      : logi  FALSE TRUE FALSE

En los dataframes, las filas también pueden tener un nombre, para darles nombre usamos la función row.names().

row.names(mi_df) <- c("A", "B", "C")
mi_df

##     ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          26  TRUE
## C   Merida          32 FALSE

El comando row.names() se puede dar como atributo cuando se construye el dataframe.

mi_df <- data.frame(ciudad = c("Morelia", "Veracruz", "Merida"),
                    Temperatura = c(27, 26, 32),
                    Playa = c(FALSE, TRUE, FALSE),
                    row.names = c("A", "B", "C"))
mi_df

##     ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          26  TRUE
## C   Merida          32 FALSE

Para acceder a los datos del dataframe es similar a la forma de los arreglos o vectores y además podemos mandar a llamar solo una columna usando el operador $.

mi_df$ciudad

## [1] "Morelia"  "Veracruz" "Merida"

mi_df[,2]

## [1] 27 26 32

mi_df[c("A","B"),]

##     ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          26  TRUE

#Cambiar la temperatura de Veracruz
mi_df[2,2] <- 33
mi_df

##     ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          33  TRUE
## C   Merida          32 FALSE

Una forma de modificar el nombre de una columna de nuestro dataframe es con la función names.

names(mi_df)[1] <- "Ciudad"
mi_df

##     Ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          33  TRUE
## C   Merida          32 FALSE

Las funciones rbind cbind que usamos con los arreglos también se pueden usar para expandir los dataframes.

nuevo_df <- data.frame(c("Monterrey", "Cancún"), c(25, 28), c(FALSE, TRUE))
nuevo_df

##   c..Monterrey....Cancún.. c.25..28. c.FALSE..TRUE.
## 1                Monterrey        25          FALSE
## 2                   Cancún        28           TRUE

#rbind(mi_df, nuevo_df)

Al no tener los mismos nombres de columnas, no se puede usar rbind para combinarlos. Esto se puede solucionar cambiando los nombres del segundo dataframe.

colnames(nuevo_df)

## [1] "c..Monterrey....Cancún.." "c.25..28."               
## [3] "c.FALSE..TRUE."

colnames(nuevo_df) <- colnames(mi_df)
colnames(nuevo_df)

## [1] "Ciudad"      "Temperatura" "Playa"

rbind(mi_df, nuevo_df)

##      Ciudad Temperatura Playa
## A   Morelia          27 FALSE
## B  Veracruz          33  TRUE
## C    Merida          32 FALSE
## 1 Monterrey          25 FALSE
## 2    Cancún          28  TRUE

Con cbind no tenemos este problema ya que lo que hacemos es agregar columnas.

info_extra <- data.frame(Habitantes = c(849053, 8063000, 892363)) 
cbind(mi_df, info_extra)

##     Ciudad Temperatura Playa Habitantes
## A  Morelia          27 FALSE     849053
## B Veracruz          33  TRUE    8063000
## C   Merida          32 FALSE     892363

Otra forma de agregar una columna es con el operador $.

mi_df$Habitantes <- c(849053, 8063000, 892363)
mi_df

##     Ciudad Temperatura Playa Habitantes
## A  Morelia          27 FALSE     849053
## B Veracruz          33  TRUE    8063000
## C   Merida          32 FALSE     892363

El operador $ también nos sirve para eliminar una columna.

mi_df$Habitantes <- NULL
mi_df

##     Ciudad Temperatura Playa
## A  Morelia          27 FALSE
## B Veracruz          33  TRUE
## C   Merida          32 FALSE

Para guardar un dataframe usamos la función write.csv.

write.csv(mi_df, file = "D:/Users/hayde/Documents/R_sites/Seminario_Estadistica/data/municipios.csv", row.names = FALSE)

Para leer el csv que acabamos de guardar usamos la función reaf.csv.

municipios <- read.csv(file = "D:/Users/hayde/Documents/R_sites/Seminario_Estadistica/data/municipios.csv", stringsAsFactors = TRUE)
municipios

##     Ciudad Temperatura Playa
## 1  Morelia          27 FALSE
## 2 Veracruz          33  TRUE
## 3   Merida          32 FALSE

municipios$ciudad

## NULL

7.1.5 Listas

Las listas son objetos ordenados de una solo longitud y sus elementos pueden ser de distinto tipo, incluso otras listas. La función para crear listas es list().

mi_lista <- list(1,"a", TRUE)
mi_lista ; class(mi_lista) ; typeof(mi_lista)

## [[1]]
## [1] 1
## 
## [[2]]
## [1] "a"
## 
## [[3]]
## [1] TRUE

## [1] "list"

## [1] "list"

Para acceder a los elementos de una lista es similar a la de los vectores e incluso se le puede dar nombres a las entradas o modificarlos como con los vectores usando la función names().

mi_lista2 <- list(mi_vector = c(1,2,3,4),
                  mi_array = array(c(1:9),dim=c(3,3)),
                  mi_booleano = TRUE)
mi_lista2

## $mi_vector
## [1] 1 2 3 4
## 
## $mi_array
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
## 
## $mi_booleano
## [1] TRUE

names(mi_lista2)

## [1] "mi_vector"   "mi_array"    "mi_booleano"

names(mi_lista2)[3] = "mi_logico"
names(mi_lista2)

## [1] "mi_vector" "mi_array"  "mi_logico"

No es necesario que todas las entradas de la lista tengan los mismos nombres.

mi_lista3 <- list(c(1:3),letra = "a", c(TRUE,FALSE))
names(mi_lista3)

## [1] ""      "letra" ""

La función length() nos devuelve la dimensión de una lista.

length(mi_lista2) ; length(mi_lista3)

## [1] 3

## [1] 3

Con la función srt() podemos conocer la estructura de la lista.

str(mi_lista2)

## List of 3
##  $ mi_vector: num [1:4] 1 2 3 4
##  $ mi_array : int [1:3, 1:3] 1 2 3 4 5 6 7 8 9
##  $ mi_logico: logi TRUE

A diferencia de los vectores y arrays, en las listas contamos con dos niveles de indexado. Con dobles corchetes accedemos a los elementos de la lista, es decir [[n]] nos devuelve el elemento $n$ de la lista y en caso de que se trate de un array, vector u otro objeto para acceder a los elementos de este objeto usamos otros corchetes, es decir objeto[[n]][p].

# Para acceder a la primera fila de la segunda entrada de la lista, la cual es 
# un array usamos:
mi_lista2[[2]][1,]

## [1] 1 4 7

class(mi_lista2[[2]])

## [1] "matrix" "array"

mi_lista2[2]

## $mi_array
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

class(mi_lista2[2])

## [1] "list"

Otra forma de acceder a los objetos de la lista es usando sus nombres o con el operador $ como en los dataframes.

mi_lista2["mi_vector"]

## $mi_vector
## [1] 1 2 3 4

mi_lista2[["mi_vector"]]

## [1] 1 2 3 4

mi_lista2$mi_array

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9

Para añadir elementos a una lista debemos ser cuidadosos con los índices que usamos, si usamos [[k]] estaríamos añadiendo un objeto en la posición $k$ de la lista y si usamos [[k]][j] estaríamos añadiendo el elemento $j$ al objeto $k$ de la lista.

mi_lista[[4]] <- c("a","b","c")
mi_lista

## [[1]]
## [1] 1
## 
## [[2]]
## [1] "a"
## 
## [[3]]
## [1] TRUE
## 
## [[4]]
## [1] "a" "b" "c"

mi_lista[[1]][2] <- 2
mi_lista

## [[1]]
## [1] 1 2
## 
## [[2]]
## [1] "a"
## 
## [[3]]
## [1] TRUE
## 
## [[4]]
## [1] "a" "b" "c"

Para eliminar elementos de una lista podemos asignar NULL a la posición de la lista, sin embargo esta asignación no hace diferencia de si usamos [[]], [] o $.

mi_lista4 <- list(c(1,2,3,4),array(c(1:4),dim = c(2,2)), c(TRUE,FALSE))
mi_lista4

## [[1]]
## [1] 1 2 3 4
## 
## [[2]]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## [[3]]
## [1]  TRUE FALSE

mi_lista4[1] <- NULL
mi_lista4

## [[1]]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## [[2]]
## [1]  TRUE FALSE

mi_lista4 <- list(c(1,2,3,4),array(c(1:4),dim = c(2,2)), c(TRUE,FALSE))
mi_lista4[[1]] <- NULL
mi_lista4

## [[1]]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## [[2]]
## [1]  TRUE FALSE

mi_lista4 <- list(mi_vec = c(1,2,3,4),mi_array = array(c(1:4),dim = c(2,2)), mi_log = c(TRUE,FALSE))
mi_lista4[["mi_array"]] <- NULL
mi_lista4

## $mi_vec
## [1] 1 2 3 4
## 
## $mi_log
## [1]  TRUE FALSE

mi_lista4 <- list(mi_vec = c(1,2,3,4),mi_array = array(c(1:4),dim = c(2,2)), mi_log = c(TRUE,FALSE))
mi_lista4["mi_array"] <- NULL
mi_lista4

## $mi_vec
## [1] 1 2 3 4
## 
## $mi_log
## [1]  TRUE FALSE

mi_lista4 <- list(mi_vec = c(1,2,3,4),mi_array = array(c(1:4),dim = c(2,2)), mi_log = c(TRUE,FALSE))
mi_lista4$mi_array <- NULL
mi_lista4

## $mi_vec
## [1] 1 2 3 4
## 
## $mi_log
## [1]  TRUE FALSE

mi_lista4 <- list(mi_vec = c(1,2,3,4),mi_array = array(c(1:4),dim = c(2,2)), mi_log = c(TRUE,FALSE))
mi_lista4[c(1,3)] <- NULL
mi_lista4

## $mi_array
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

mi_lista4 <- list(mi_vec = c(1,2,3,4),mi_array = array(c(1:4),dim = c(2,2)), mi_log = c(TRUE,FALSE))
mi_lista4[-c(1,3)]

## $mi_array
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

Para combinar dos listas usamos el operador que se usa para concatenar vectores c().

lista1 <- list(c(1,2,3),c("a","b"))
lista2 <- list(array(c(1:4),dim=c(2,2)), c(TRUE,FALSE))

lista3 <- c(lista1, lista2)
lista3

## [[1]]
## [1] 1 2 3
## 
## [[2]]
## [1] "a" "b"
## 
## [[3]]
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4
## 
## [[4]]
## [1]  TRUE FALSE

class(lista3)

## [1] "list"

#Ejercicio: Crea una lista y concatenala con la lista mi_lista3. Modifica la entrada 3,1 y el nombre de la entrada 2 de la lista.

7.1.6 Factores

Los factores nos ayudan a representar los niveles de los datos, pueden parecer caracteres pero en realidad son niveles. Por ejemplo, se pueden usar para representar el género, continentes, razas de algún animal, etc.

gatos <- c("Siames", "Calico", "Angora", "Carey")
str(gatos)

##  chr [1:4] "Siames" "Calico" "Angora" "Carey"

categorias_gatos <- factor(gatos)
class(categorias_gatos)

## [1] "factor"

str(categorias_gatos)

##  Factor w/ 4 levels "Angora","Calico",..: 4 2 1 3

typeof(gatos); typeof(categorias_gatos)

## [1] "character"

## [1] "integer"

Para conocer los niveles de nuestro objeto usamos la función levels() y cuantos niveles tenemos nlevels().

levels(categorias_gatos); nlevels(categorias_gatos)

## [1] "Angora" "Calico" "Carey"  "Siames"

## [1] 4

Los factores se ordenan alfabéticamente.

niveles <- c("alto", "medio", "bajo")
factor(niveles)

## [1] alto  medio bajo 
## Levels: alto bajo medio

factor(niveles, order = TRUE, levels = c("bajo", "medio", "alto"))

## [1] alto  medio bajo 
## Levels: bajo < medio < alto

niveles2 <- factor(niveles, order = TRUE, levels = c("bajo", "medio", "alto"))
niveles2; as.numeric(niveles2)

## [1] alto  medio bajo 
## Levels: bajo < medio < alto

## [1] 3 2 1

7.1.7 Atributos de objetos

Los atributos de los objetos los podemos obtener de la siguiente forma: - Modo: Cualquier tipo de entidad que maneja R, se usa la función mode(objeto). - Tipo: Tipo de dato: entero, caracter, double, etc. Se usa la función typeof(objeto). - Nombres: etiquetas de los elementos individuales de un vector o lista. Se usa la función names(objeto). - Dimensiones: Dimensión de los arreglos. Se usa la función dim(objeto). Esta función devuelve dos valores: el primero es el número de filas, el segundo el de columnas. - Dimnames: Nombres de las dimensiones de los arrays. Se usa la función dimnames(objeto). - Clase: Vector alfanumérico con la lista de las clases del objeto. Se usa la función class(objeto). - Longitud: Longitud de cualquier estructura. Se usa la función length(objeto).

typeof(mi_vector)

## [1] "character"

El operador ls() nos permite listar todas las variables y funciones de nuestro ambiente global, sin embargo los objetos que comienzan con . no son listados, para listar estas variables se utiliza ls(all.names = TRUE).

ls()

##  [1] "A"                  "B"                  "categorias_gatos"  
##  [4] "clases"             "gatos"              "indices"           
##  [7] "info_extra"         "lista1"             "lista2"            
## [10] "lista3"             "Logaritmo"          "matriz_ceros"      
## [13] "matriz1"            "matriz2"            "matriz3"           
## [16] "mi_array"           "mi_array1"          "mi_array2"         
## [19] "mi_array3"          "mi_df"              "mi_lista"          
## [22] "mi_lista2"          "mi_lista3"          "mi_lista4"         
## [25] "mi_vector"          "mi_vector2"         "mis_calificaciones"
## [28] "municipios"         "niveles"            "niveles2"          
## [31] "nuevo_df"           "raiz_x"             "w"                 
## [34] "workingDir"         "x"                  "y"                 
## [37] "z"

Para borrar un objeto usamos rm(objeto).

rm(mi_vector)

En el caso de querer eliminar todos los objetos de nuestro ambiente, usamos rm(list = ls() ). Es importante señalar que se debe usar el operador = para asignar al objeto list todos los objetos que estén en ls() en lugar del operador <-.

7.1.8 Ejercicios

Crea una base de datos de los asistentes a la clase y dale el nombre estudiantes, almacena datos como nombre, edad, lugar de origen, grado, o algunos otros de tal forma que la base de datos tenga variables de todos los tipos, numéricos, factores, lógicos y caracteres.

Usando la base de datos estudiantes, extrae las columnas de los estudiantes con edad mayor al promedio de las edades y aquellos estudiantes del mismo grado.
Extrae las ciudades o regiones de aquellos estudiantes mayores a la edad promedio.
Ordena la base de datos usando alguna variable cuantitativa.
Crea una lisa con los elementos de la base de datos estudiantes y da un nombre a las entradas de la lista y accede a tu nombre y edad como subelementos de la lista.

Usando la ayuda de R, busca como se pueden redondear los números $2.5$, $4.8$, $9,2$. ¿Cuáles fueron los resultados de redondear? Ahora, trata de redondear a dos decimales los siguientes números: $4.765$, $3.231$, $9.769$.
Crea una vector con las letras A M A B M M B A B B, donde A significa Alto, B bajo y M medio. Convierte las entradas del vector a factores y especifica que A > M > B.
Carga la base de datos CO2 del paquete datasets usando data("CO2"). Explora la base de datos y revisa que tipo de datos tiene cada columna.

Calcula el promedio de las tasas de absorción de CO2 en Quebec (uptake).
Obtén el máximo y mínimo de las concentraciones de CO2 para las plantas chilled.
Para las plantas Ms2, ¿cuántos niveles de concentración ambiental de CO2 se midieron?.
Para plantas non-chilled, cuando la concentración es 500, ¿cuáles son los niveles de absorción uptake?

7.2 Estructuras de control

Las estructuras de control se refieren a como hacemos que un algoritmo tome alguna decisión o camino dependiendo de las condiciones que se le especifiquen y realice ciclos o repeticiones.

Vamos a ver dos tipos de estructuras de control. La primera el condicional if donde ciertas instrucciones son ejecutadas dada la veracidad de la condición que actúa como un parámetro de control. La segunda se trata de los ciclos, los cuales repiten ciertas instrucciones varias veces, de este tipo de estructuras de control tenemos el ciclo for que se usa cuando las repeticiones se realizan un número fijo de veces (el parámetro de control) y el ciclo while cuando las iteraciones no se especifican a priori pero continua evaluándose mientras alguna condición no se alcance.

7.2.1 Condicional `if`

La palabra clave if siempre evalúa una expresión lógica y cuando dicha expresión de por resultado el valor TRUE, se ejecutará el código indicado a continuación del if entre llaves. En caso de que el resultado sea FALSE, ignorará lo que se encuentre inmediatamente del if entre llaves y continuará con la siguiente instrucción.

# if
if (condicion es TRUE) {
  instrucción
}

# if ... else
if (condicion es TRUE) {
  instrucción
} else {
  instruccion alternativa
}

# if ... else if ... else
if (condicion es TRUE) {
  instrucción
} else if (condicion es TRUE) {
  instruccion alternativa
} else {
  ultima condicion
}

Por ejemplo, vamos a crear una variable y asignarle un valor, después vamos imprimir en pantalla si la variable tiene cierto valor.

x <- 8

if (x >= 10) {
  print(" x es más grande o igual a 10")
}
x

## [1] 8

Como $x$ no es más grande que 10, entonces no nos devuelve ningún mensaje.

x <- 8

if (x >= 10) {
  print(" x es más grande o igual a 10")
} else {
  print(" x es menor que 10")
}

## [1] " x es menor que 10"

## [1] 8

Para verificar varias condiciones podemos usar else if

x <- 8

if (x >= 10) {
  print(" x es más grande o igual a 10")
} else if (x > 5) {
  print("x es mayor que 5 pero menor que 10")
} else {
  print(" x es menor que 10")
}

## [1] "x es mayor que 5 pero menor que 10"

## [1] 8

edad <- readline(prompt = "Escribe tu edad:")

if (edad >= 30 ) {
  print("Tal vez tenemos la misma edad")
} else{
  print("Soy mayor que tu")
}

# Ejercicio: crea un ciclo if que pregunte un número y que devuelva el mensaje de si el número es positivo, negativo o cero.

También se pueden crear ciclos anidados.

dato_texto = readline(prompt="Ingresa un número: ")
dato  <- as.numeric(dato_texto)
if(is.na(dato) == FALSE){
    print('Es un número.')
    if(dato < 0){
        print('Es negativo.')
    } else if(dato > 0){
        print('Es positivo.')
    } else{
        print('Es cero')
    }
} else{
    print('No es un número.')
}

#Convierte el if anidado anterior en uno no anidado.

Existe una función adicional llamada ifelse(), la estructura de esta es ifelse(condicion is TRUE, instruccion1, instruccion alternativa).

x <- -2

ifelse(x < 0, "x es un número negativo", "x es un número positivo o cero")

## [1] "x es un número negativo"

Tres funciones que son de gran ayuda para verificar condiciones son all(), any(), which().

edades <- c(12, 11, 24, 30, 5, 27, 12)

all(edades >= 25) ; any(edades == 30); which(edades == 12)

## [1] FALSE

## [1] TRUE

## [1] 1 7

7.2.2 Ciclo `for`

La función for() realiza un bloque de códigos tantas veces como se indique un argumento. Los objetos de tipo iterable, es decir los que se pueden recorrer son los vectores y las listas. La sintaxis de un for es la siguiente:

for (contador in vector_indices){
  instrucciones a ejecutar
}

El vector de índices se define antes de las instrucciones entre {} o dentro de los (). Por ejemplo,

for (i in 1:10){
  print(i)
}

## [1] 1
## [1] 2
## [1] 3
## [1] 4
## [1] 5
## [1] 6
## [1] 7
## [1] 8
## [1] 9
## [1] 10

Al terminar el ciclo for(), el valor de la varible i toma el último valor de la lista de índices.

## [1] 10

Vamos a crear un vector vacío y que después se rellene con la suma acumulativa de los enteros consecutivos en el vector.

vec <- c()
vec

## NULL

s <- 0
for (i in 1:10){
  s <- s + i
  vec[i] <- s
}
vec

##  [1]  1  3  6 10 15 21 28 36 45 55

impares <- 2*(1:10)-1

for (i in impares){
  print(i)
}

## [1] 1
## [1] 3
## [1] 5
## [1] 7
## [1] 9
## [1] 11
## [1] 13
## [1] 15
## [1] 17
## [1] 19

También se pueden usar valores lógicos como sigue.

for (i in c(TRUE, FALSE, TRUE)){
  print(TRUE == i)
}

## [1] TRUE
## [1] FALSE
## [1] TRUE

Las estructuras de control se pueden combinar. Por ejemplo, vamos a crear un condicional con un for y un if que nos regrese el mensaje de si un estudiante alcanzó al menos 5 puntos en un examen.

puntos <- c(10,4, 6,2,4, 7, 5, 9, 8, 0)
for (puntaje in puntos){
  if (puntaje < 5 ){
    print("Reprobó")
  } else {
    print("Aprobó")
  }
}

## [1] "Aprobó"
## [1] "Reprobó"
## [1] "Aprobó"
## [1] "Reprobó"
## [1] "Reprobó"
## [1] "Aprobó"
## [1] "Aprobó"
## [1] "Aprobó"
## [1] "Aprobó"
## [1] "Reprobó"

# Ejercicio: crea un ciclo para calcular el factorial de un número.
# Hint: usa un if y un for anidados y define dos variables n<-número al cúal se le va a calcular el factorial y fac <- iniciala en 1 y esa será el resultado del factrorial de n.

7.2.3 Ciclo `while`

El ciclo while() se usa para realizar un bloque de código recursivamente mientras no se alcance cierta condición. Si el resultado de la evaluación es FALSE entonces no se realizará la instrucción. La estructura del condicional while() es como sigue.

while(expresion logica){
  instrucciones a ejecutar
}

El siguiente ejemplo imprime en pantalla un número mientras este no sea mayor a 10.

i <- 0
while (i < 10){
  print(c(i,"es menor a 10"))
  i <- i + 1
}

## [1] "0"             "es menor a 10"
## [1] "1"             "es menor a 10"
## [1] "2"             "es menor a 10"
## [1] "3"             "es menor a 10"
## [1] "4"             "es menor a 10"
## [1] "5"             "es menor a 10"
## [1] "6"             "es menor a 10"
## [1] "7"             "es menor a 10"
## [1] "8"             "es menor a 10"
## [1] "9"             "es menor a 10"

Igual que con el condicional for(), i es una variable que al finalizar el ciclo tiene el último valor con el que fue evaluada, en este caso:

## [1] 10

Se debe de tener cuidado de modificar el valor de la variable a iterar para no terminar con un condicional infinito.

i <- 0
while (i < 10){
  print(c(i,"es menor a 10"))
  #i <- i + 1
}

El siguiente ciclo nos devuelve el primer número cuyo cuadrado exceda el número dado.

num_dado <- 2023
numero <- 0
while (numero ^ 2 <= num_dado) {
  numero = numero + 1
}
numero

## [1] 45

Los while() se pueden emplear con caracteres.

frase <- "Hola a todos"
n=1
lista <- list()
while (n <= nchar(frase)) {
  lista[[n]] = list(recorridos = substr(frase,1, n), num_caracteres = n)
  n = n + 1
}
lista

## [[1]]
## [[1]]$recorridos
## [1] "H"
## 
## [[1]]$num_caracteres
## [1] 1
## 
## 
## [[2]]
## [[2]]$recorridos
## [1] "Ho"
## 
## [[2]]$num_caracteres
## [1] 2
## 
## 
## [[3]]
## [[3]]$recorridos
## [1] "Hol"
## 
## [[3]]$num_caracteres
## [1] 3
## 
## 
## [[4]]
## [[4]]$recorridos
## [1] "Hola"
## 
## [[4]]$num_caracteres
## [1] 4
## 
## 
## [[5]]
## [[5]]$recorridos
## [1] "Hola "
## 
## [[5]]$num_caracteres
## [1] 5
## 
## 
## [[6]]
## [[6]]$recorridos
## [1] "Hola a"
## 
## [[6]]$num_caracteres
## [1] 6
## 
## 
## [[7]]
## [[7]]$recorridos
## [1] "Hola a "
## 
## [[7]]$num_caracteres
## [1] 7
## 
## 
## [[8]]
## [[8]]$recorridos
## [1] "Hola a t"
## 
## [[8]]$num_caracteres
## [1] 8
## 
## 
## [[9]]
## [[9]]$recorridos
## [1] "Hola a to"
## 
## [[9]]$num_caracteres
## [1] 9
## 
## 
## [[10]]
## [[10]]$recorridos
## [1] "Hola a tod"
## 
## [[10]]$num_caracteres
## [1] 10
## 
## 
## [[11]]
## [[11]]$recorridos
## [1] "Hola a todo"
## 
## [[11]]$num_caracteres
## [1] 11
## 
## 
## [[12]]
## [[12]]$recorridos
## [1] "Hola a todos"
## 
## [[12]]$num_caracteres
## [1] 12

7.3 Funciones y Operadores

En R al igual que en otros lenguajes de programación podemos crear nuestras propias funciones.

La estructura de una función en R es la siguiente:

mi_funcion <- function(parametros){
  acciones
  resultado a regresar
}

Por ejemplo, supongamos que necesitamos calcular repetidamente el valor de la función $f(x)=x^2/(x-1)$.

fx <- function(x){
  (x*x)/(x-1)
}

Entonces para evaluarla en algún número solo usamos la intrucción:

fx(5)

## [1] 6.25

Supongamos que dado un vector, queremos calcular la suma de sus entradas, restarle el elemento máximo y el mínimo.

mi_funcion <- function(vec){
  suma <- sum(vec)
  maximo <- max(vec)
  minimo <- min(vec)
  return(suma - maximo - minimo)
}

Aplicamos la función a un vector:

mi_funcion(c(1,3,6,8,9))

## [1] 17

En las funciones podemos indicar la operación a realizar como en el ejemplo uno o escribir la palabra reservada return para que nos regrese ese resultado.

Las funciones pueden recibir más de un parámetro como en el caso de funciones matemáticas en dos o más variables. Por ejemplo, supongamos que queremos crear la función $g(x,y)= x^2 - y^2$.

gxy <- function(x,y) {
  x^2 -y^2
}

gxy(2,1)

## [1] 3

A las funciones también podemos pasarle parámetros opcionales como en otras funciones que ya hemos utilizado como matrix. Por ejemplo, supongamos que queremos crear una función que nos cree vectores o matrices dependiendo de los parámetros que le proporcionemos.

vec.mat <- function(a, b=2, flag = FALSE){
  if (flag){
    matrix(1:a, nrow = b)
  } else{
    1:a
  }
}

Por ejemplo, le podemos dar solo el parámetro a:

vec.mat(4)

## [1] 1 2 3 4

Y es lo mismo a indicar el parámetro a y flag=FALSE:

vec.mat(4, FALSE)

## [1] 1 2 3 4

En cambio, si cambiamos el parámetro de flag=TRUE:

vec.mat(8,4,TRUE)

##      [,1] [,2]
## [1,]    1    5
## [2,]    2    6
## [3,]    3    7
## [4,]    4    8

Si no queremos proporcionar el parámetro b pero si queremos una matriz debemos especificar que TRUE es el valor de flag:

vec.mat(8,flag=TRUE)

##      [,1] [,2] [,3] [,4]
## [1,]    1    3    5    7
## [2,]    2    4    6    8

Una función en R solo puede regresar un objeto pero si queremos que nos regrese más de un objeto podemos usar listas para almacenar los resultados.

elementos <- function(x) list(len=length(x),total=sum(x),
                          promedio=mean(x))

datos <- 1:10
elementos(datos)

## $len
## [1] 10
## 
## $total
## [1] 55
## 
## $promedio
## [1] 5.5

resultado <- elementos(datos)
names(resultado); resultado$len

## [1] "len"      "total"    "promedio"

## [1] 10

En el caso de que queramos obtener algún mensaje de error cuando el argumento de nuestra función no sea lo esperado podemos usar la función stop.

fxx <- function(x){
  if (!is.numeric(x)){
    stop("x debe ser un número")
  } 
  result <- (x*x)/(x-1)
  return(result)
}

fxx("a")

Otro argumento que funciona de forma similar a stop es stopifnot(), este se usa en el caso de que no se quieran verificar varias condiciones.

fxx <- function(x){
  stopifnot(is.numeric(x))
  result <- (x*x)/(x-1)
  return(result)
}

fxx("a")

7.3.1 Ejercicios

Crea un vector que contenga los 7 días de la semana. Haz una función que dado un número del 1 al 7, imprima el día de la semana correspondiente.
Crea una función que dado un número del 1 al 12 imprima el nombre del mes correspondiente.
Crea una función que calcule las raices de un polinomio cuadrático.
Considera la función

g <- function(x, y) x ^ 2 - y / 5

Aplícala a: g(1 : 2, 2 : 3) y g(1 : 4, 1 : 5). ¿Qué está realizando la función al aplicarla a datos?

Escribe una función que tome cualquier dataframe con entradas numéricas y nos devuelva el mismo dataframe con un renglón con el promedio de cada columna.

7.4 Scripts

Un script es una colección de varias instrucciones de R escritas en un archivo. La extensión de los script en R es .r o .R. En los scripts podemos colocar comentarios, paquetes, instrucciones de tal forma que pueda ser ejecutado sin problemas. Para ejecutar un script usamos la instrucción source("nombre.R"), en caso de no estar el script en nuestro directorio de trabajo debemos fijarlo o poner la ruta completa al script.

Por ejemplo, vamos a crear un script llamado mi_script.R con dos variables y que calcule su producto. Para ejecutar el script vamos a escribir en la consola source("mi_script.R").

# Mi primer script

a = 5

b = 6

c = a*b

print(c)

Nota: Para desinstalar algún paquete o instalar un paquete indicando que se instalen todas las dependencias se realizar lo siguiente:

remove.packages(c("ggplot2"))
install.packages('ggplot2', dependencies = TRUE)

7.5 Manipulación de bases de datos

El manejo de bases de datos es uno de los puntos clave o principales al momento de realizar un análisis de datos. En ocasiones, lo más díficil es tener una base de datos que sea posible manipular. El primer paso es tener una base de datos, después importarla a R y manipularla de tal forma que podamos trabajar con ella. En la primera parte del curso, comenzamos a trabajar con objetos data.frame, otro tipo de objetos son los data.table que tienen mejor poder de procesamiento y los tibbles que incorporan otras características a los datos y que pueden ser de ayuda.

Para importar un archivo .csv recordemos que usamos read.csv(), esta función nos permite indicarle si tiene encabezados con header= TRUE, el tipo de delimitadores con sep=";" entre otras opciones.

iris <- read.csv("D:/Users/hayde/Documents/R_sites/Computo_Cientifico/data/iris.csv", header = TRUE, sep = ",")

Para exportar un data frame usamos la función write.csv().

write.csv(iris, "iris2.csv", row.names = FALSE)

Otros tipos de archivos que podemos cargar son .txt, .dat, .tsv y podemos usar las funciones read.table() o read.delm().

Otro paquete que se puede usar es library(readr). En este, se encuentran funciones como read_csv() para leer archivos delimitados por ,, está la función read_csv2() para leer archivos delimitados por ;, la función read_tsv() para archivos separados por tabulador y read_delim() para especificar los delimitadores. La función read_csv() nos imprime en pantalla el tipo de columnas de la base de datos, a esta función le podemos pasar un archivo csv o podemos darle línea por línea el archivo, y por default considerará la primera línea como los nombres de las columnas.

library(readr)
read_csv("x,y,z
1,2,3
4,5,6")

## # A tibble: 2 × 3
##       x     y     z
##   <dbl> <dbl> <dbl>
## 1     1     2     3
## 2     4     5     6

Si queremos evitar las primeras líneas, podemos usar el argumento skip = n o indicarle que lo que está con # es un comentario y no va en la base de datos.

read_csv(" Comentario que no va en la base de datos
a,b,c
1,2,3
4,5,6", skip= 1)

## Rows: 2 Columns: 3
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (3): a, b, c
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

## # A tibble: 2 × 3
##       a     b     c
##   <dbl> <dbl> <dbl>
## 1     1     2     3
## 2     4     5     6

read_csv("# Algun comentario de la base de datos
a,b,c
1,2,3
4,5,6", comment = "#")

## Rows: 2 Columns: 3
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (3): a, b, c
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.

## # A tibble: 2 × 3
##       a     b     c
##   <dbl> <dbl> <dbl>
## 1     1     2     3
## 2     4     5     6

El paquete data.table nos ayuda a optimizar el guardar e importar grandes bases de datos. Las funciones para importar o guardar las bases de datos en este paquete son fread() y fwrite. Estas funciones se pueden usar con varios tipos de archivos no solo con .csv, además por lo general reconoce los separadores que usan.

library(data.table)
iris_table <- fread("D:/Users/hayde/Documents/R_sites/Computo_Cientifico/data/iris.csv", header = TRUE)

En el caso de archivos .xlsx, usamos el paquete readxl y la función para importar archivos es read_excel().

7.5.1 `tibbles`

Los tibbles son otro tipo de objetos de R del paquete tidyverse. Vamos a convertir el data frame iri en un objeto tibble usando la función as_tibble

library(tidyverse)
as_tibble(iris)

## # A tibble: 150 × 5
##    Sepal.Length Sepal.Width Petal.Length Petal.Width Species
##           <dbl>       <dbl>        <dbl>       <dbl> <chr>  
##  1          5.1         3.5          1.4         0.2 setosa 
##  2          4.9         3            1.4         0.2 setosa 
##  3          4.7         3.2          1.3         0.2 setosa 
##  4          4.6         3.1          1.5         0.2 setosa 
##  5          5           3.6          1.4         0.2 setosa 
##  6          5.4         3.9          1.7         0.4 setosa 
##  7          4.6         3.4          1.4         0.3 setosa 
##  8          5           3.4          1.5         0.2 setosa 
##  9          4.4         2.9          1.4         0.2 setosa 
## 10          4.9         3.1          1.5         0.1 setosa 
## # ℹ 140 more rows

En estos objetos, cada columna ya tiene especificado de que tipo de datos se trata, además solo nos despliega las primeras 10 filas.

Para crear un tibble es similar a como creamos dataframes.

tibble(x = 1:5 , 
       y = 6:10, 
       z= x*y)

## # A tibble: 5 × 3
##       x     y     z
##   <int> <int> <int>
## 1     1     6     6
## 2     2     7    14
## 3     3     8    24
## 4     4     9    36
## 5     5    10    50

Por default, coloca los nombres de las columnas y nunca le pone nombres a las filas. En estos objetos, es posible colocar nombres no válidos para R como símbolos, números, etc.

tibble(`:)` = "sonrisa" , 
       ` ` = "espacio", 
       `3c` = "números")

## # A tibble: 1 × 3
##   `:)`    ` `     `3c`   
##   <chr>   <chr>   <chr>  
## 1 sonrisa espacio números

Otra forma de crear estos objetos es con la función tribble, con esta función se puede especificar por renglón las entradas del objeto, se comienza escribiendo con ~ nombre el nombre de las columnas y después se especifican las entradas separadas por coma:

tribble(
  ~A, ~B, ~C,
  #--|--|----
  "x", 1, 1.5,
  "y", 2, 2.5
)

## # A tibble: 2 × 3
##   A         B     C
##   <chr> <dbl> <dbl>
## 1 x         1   1.5
## 2 y         2   2.5

La forma en la que se accede a columnas es igual que en los data.frame, usando $ o [[nombre]].

7.5.2 Paquete `plyr`

Muchas veces, tenemos nuestros datos y queremos agregar columnas o cambiar la forma de presentarlos.

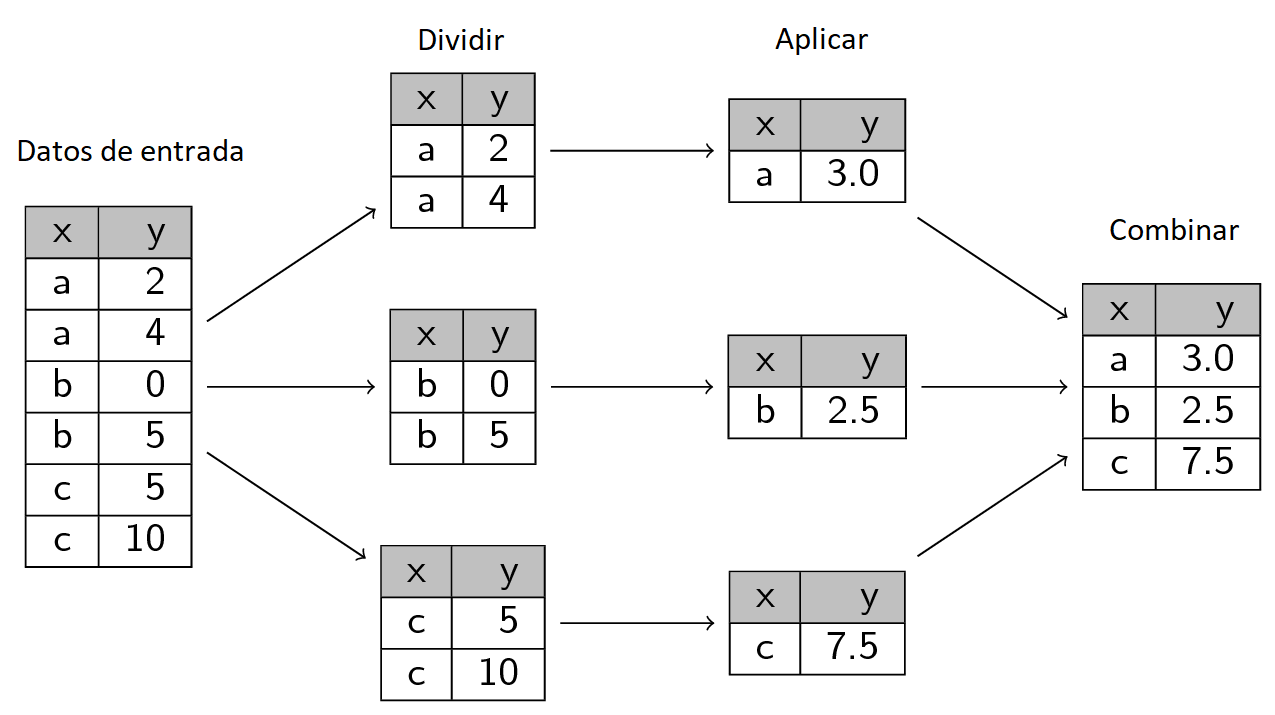
Imagen de Software Carpentry

El paquete plyr contiene varias funciones que nos ayudan a resolver el problema de dividir, aplicar y combinar las bases de datos. Funciona con listas, data frames y arreglos.

Imagen de Software Carpentry

La estructura de estas funciones es como sigue:

xxply(.data, .variables, .fun)

Supongamos que en la base de datos gapminder y queremos calcular la media de la columna gdp que se optiene con la función calcGDP.

library(gapminder)
gapminder <- gapminder::gapminder

calcGDP <- function(dat, year=NULL, country=NULL) {
  if(!is.null(year)) {
    dat <- dat[dat$year %in% year, ]
  }
  if (!is.null(country)) {
    dat <- dat[dat$country %in% country,]
  }
  gdp <- dat$pop * dat$gdpPercap
  
  new <- cbind(dat, gdp=gdp)
  return(new)
}

library(plyr)

## ------------------------------------------------------------------------------

## You have loaded plyr after dplyr - this is likely to cause problems.
## If you need functions from both plyr and dplyr, please load plyr first, then dplyr:
## library(plyr); library(dplyr)

## ------------------------------------------------------------------------------

## 
## Attaching package: 'plyr'

## The following objects are masked from 'package:dplyr':
## 
##     arrange, count, desc, failwith, id, mutate, rename, summarise,
##     summarize

## The following object is masked from 'package:purrr':
## 
##     compact

ddply(.data = calcGDP(gapminder),
      .variables = "continent",
      .fun = function(x) mean(x$gdp))

##   continent           V1
## 1    Africa  20904782844
## 2  Americas 379262350210
## 3      Asia 227233738153
## 4    Europe 269442085301
## 5   Oceania 188187105354

ddply(calcGDP(gapminder),"continent",
      function(x) mean(x$gdp))

##   continent           V1
## 1    Africa  20904782844
## 2  Americas 379262350210
## 3      Asia 227233738153
## 4    Europe 269442085301
## 5   Oceania 188187105354

¿Si queremos el resultado como lista, que función deberíamos usar?

En las variables, puede ser que a veces queramos agrupar por no solo una, en ese caso colocamos todas las variables como vector.

ddply(.data = calcGDP(gapminder),
      .variables = c("continent","year"),
      .fun = function(x) mean(x$gdp))

##    continent year           V1
## 1     Africa 1952   5992294608
## 2     Africa 1957   7359188796
## 3     Africa 1962   8784876958
## 4     Africa 1967  11443994101
## 5     Africa 1972  15072241974
## 6     Africa 1977  18694898732
## 7     Africa 1982  22040401045
## 8     Africa 1987  24107264108
## 9     Africa 1992  26256977719
## 10    Africa 1997  30023173824
## 11    Africa 2002  35303511424
## 12    Africa 2007  45778570846
## 13  Americas 1952 117738997171
## 14  Americas 1957 140817061264
## 15  Americas 1962 169153069442
## 16  Americas 1967 217867530844
## 17  Americas 1972 268159178814
## 18  Americas 1977 324085389022
## 19  Americas 1982 363314008350
## 20  Americas 1987 439447790357
## 21  Americas 1992 489899820623
## 22  Americas 1997 582693307146
## 23  Americas 2002 661248623419
## 24  Americas 2007 776723426068
## 25      Asia 1952  34095762654
## 26      Asia 1957  47267432088
## 27      Asia 1962  60136869012
## 28      Asia 1967  84648519224
## 29      Asia 1972 124385747313
## 30      Asia 1977 159802590186
## 31      Asia 1982 194429049919
## 32      Asia 1987 241784763369
## 33      Asia 1992 307100497486
## 34      Asia 1997 387597655323
## 35      Asia 2002 458042336179
## 36      Asia 2007 627513635079
## 37    Europe 1952  84971341466
## 38    Europe 1957 109989505140
## 39    Europe 1962 138984693095
## 40    Europe 1967 173366641137
## 41    Europe 1972 218691462733
## 42    Europe 1977 255367522034
## 43    Europe 1982 279484077072
## 44    Europe 1987 316507473546
## 45    Europe 1992 342703247405
## 46    Europe 1997 383606933833
## 47    Europe 2002 436448815097
## 48    Europe 2007 493183311052
## 49   Oceania 1952  54157223944
## 50   Oceania 1957  66826828013
## 51   Oceania 1962  82336453245
## 52   Oceania 1967 105958863585
## 53   Oceania 1972 134112109227
## 54   Oceania 1977 154707711162
## 55   Oceania 1982 176177151380
## 56   Oceania 1987 209451563998
## 57   Oceania 1992 236319179826
## 58   Oceania 1997 289304255183
## 59   Oceania 2002 345236880176
## 60   Oceania 2007 403657044512

Tal vez, esta forma de visualizar esa información no es adecuado y nos conviene visualizarlo como un data.frame ¿qué función usaríamos?

Si queremos hacer algun loop for, usar las funciones del paquete que tienen _ puede ser mucho más rápido.

d_ply(.data = calcGDP(gapminder),
      .variables = "continent",
      .fun = function(x){
        media <- mean(x$gdpPercap)
        print(paste(
          "La media de GDP per capita de" , unique(x$continent), "es", 
          format(media, big.mark=",")
        ))
      } 
      )

## [1] "La media de GDP per capita de Africa es 2,193.755"
## [1] "La media de GDP per capita de Americas es 7,136.11"
## [1] "La media de GDP per capita de Asia es 7,902.15"
## [1] "La media de GDP per capita de Europe es 14,469.48"
## [1] "La media de GDP per capita de Oceania es 18,621.61"

7.5.2.1 Ejercicios

Calcula la media la esperanza de vida por continente y año y preséntala como un data.frame. ¿Cuál continente tuvo la mayor y menor esperanza de vida en el año 1952 y 2007?
Carga la base de datos iris, y crea un data.frame con la media, el valor máximo y mínimo de cada una de las variables agrupado por especie.
Explora la página y busca una base de datos donde puedas aplicar las funciones anteriores y que tenga sentido lo que estás presentando de resultados.

7.5.3 Paquete `dplyr`

El paquete dplyr contiene varias funciones que nos ayudan a realizar operaciones en los data.frames de tal forma que reduce el repetir estas operaciones o cometer errores al momento de combinar los resultados. Algunas de las funciones de este paquete son:

filter()
select()
count()
arrange()
group_by()
mutate()
summarize()
transmute()
ungroup()
slice_min()
slice_max()
left_join()

Instalamos el paquete dplyr y lo cargamos.

library(dplyr)
library(reshape2) # para modificar el formato del dataframe

Nota: Este paquete tiene algunos conflictos con el paquete plyr dependiendo de cual se carga primero o algunas funciones que tienen en común y que sus argumentos son diferentes. Para evitar esta confusión se puede usar la sintaxis dplyr::funcion.

Vamos a trabajar con el set de datos de Marvel vs DC, ve a la página y descarga las bases de datos en formato csv.

Cargamos las 3 bases de datos de Marvel vs DC. Vamos a usar la instrucción na.strings = c("-", "-99") para sustituir los valores - y 99 por NA.

infoHeroes <- read.csv("D:/Users/hayde/Documents/R_sites/Computo_Cientifico/data/heroesInformation.csv", na.strings = c("-", "-99", "-99.0")) 
infoPowers <- read.csv("D:/Users/hayde/Documents/R_sites/Computo_Cientifico/data/superHeroPowers.csv")
infoStats <- read.csv("D:/Users/hayde/Documents/R_sites/Computo_Cientifico/data/charactersStats.csv", na.strings = "")

Unificamos el nombre de la columna en las 3 bases de datos del nombre de los personajes a Name.

colnames(infoHeroes)[2] <- "Name"
colnames(infoPowers)[1] <- "Name"

7.5.3.1 `filter()`

El verbo filter nos permite filtrar las columnas por una o más condiciones. Por ejemplo, si queremos seleccionar de la base de datos infoHeroes solo los personajes de DC o Marvel, realizariamos lo siguiente:

Marvel <- infoHeroes %>% 
  filter(Publisher=="Marvel Comics")

head(Marvel)

DC <- infoHeroes %>% 
  filter(Publisher=="DC Comics")

head(DC)

DC_Marvel <- infoHeroes %>% 
  filter(Publisher %in% c("DC Comics", "Marvel Comics"))

head(DC_Marvel)

Si exploramos la base de datos, vamos a ver que existen personajes duplicados. Esto también lo podemos obtener con la siguiente instrucción.

duplicated(DC_Marvel$Name)
dim(DC_Marvel)

Usando el mismo verbo de filter podemos eliminar los personajes duplicados como sigue.

DC_Marvel <- DC_Marvel %>%
  filter(!duplicated(Name))

dim(DC_Marvel)

7.5.3.2 `select()`

El verbo select nos permite seleccionar columnas de nuestro dataframe.

DC_Marvel_s <- DC_Marvel %>%
  select(Name, Gender, Race, Publisher)

Ejercicio: ¿Qué otras columnas son de tu interés de la base de datos o de las otras dos bases de datos? ¿Como las seleccionarías?

Ejercicio: Busca la ayuda de ?select_helpers. ¿Cómo podrías usar alguno de estos en la base de datos?

7.5.3.3 `count()`

El verbo count nos permite contar cuantos elementos de cada tipo hay en las columnas que indiquemos. Por ejemplo, si volvemos a cargar la base de datos inicial de DC_Marvel, con la siguiente instrucción podríamos obtener de nuevo cuales son los personajes que están repetidos.

personajes <- DC_Marvel %>% 
  count(Name)

Si queremos saber cuantos personajes hombres y mujeres hay en la base de datos, realizariamos lo siguiente.

DC_Marvel %>% 
  count(Gender)

También podemos especificar más de una columna. Por ejemplo, para saber cuantos personajes hay de cada compañía y de que géndero son.

DC_Marvel %>% 
  count(Publisher, Gender)

¿Qué pasa si intercambiamos el orden de las variables en el verbo count?

Ejercicio: De la base de datos infoStats, como encontrarías cuántos personajes son buenos y cuántos son malos? ¿Y de cada compañía?

7.5.3.4 `arrange()`

El verbo arrange nos permite ordenar la base de datos de acuerdo a alguna varible ya sea en orden ascendente o descendente indicando la opción desc.

Seleccionaremos primero las columnas Name, Gender, Race, Height, Publisher.

DC_Marvel_H <- DC_Marvel %>%
  select(Name, Gender, Race, Height, Publisher)

Para odernarlos en orden ascendente por la columna Height hacemos lo siguiente.

DC_Marvel_H %>%
  arrange(Height)

Los verbos los podemos anidar usando el operador pipe %>%. Por ejemplo podemos realizar las dos instrucciones anteriores de una sola vez.

DC_Marvel %>%
  select(Name, Gender, Race, Height, Publisher) %>%
  arrange(Height)

Algunos operadores no importa el orden en que los usemos.

DC_Marvel %>%
  arrange(desc(Height)) %>%
  select(Name, Gender, Race, Height, Publisher)

7.5.3.5 `group_by()`

El verbo group_by nos permite agrupar por alguna variable.

DCM <- DC_Marvel_H %>%
  group_by(Publisher)

Este verbo nos devuelve en realidad una lista donde cada elemento es un data.frame en el que las filas corresponden a la variable por la que se agrupo.

str(DC_Marvel_H %>%
  group_by(Publisher))

Este verbo visualmente no hace nada, tiene efecto cuando agregamos algún otro verbo. Por ejemplo, vamos a contar cuantos personajes son Humanos de cada compañía.

DC_Marvel_H %>%
  group_by(Publisher) %>%
  count(Race == "Human")

7.5.3.6 `sumarize()`

El verbo sumarize() nos permite realizar alguna operación sobre las variables y/o agregarlas a la base de datos. Algunas de las operaciones que se pueden usar son:

mean()
max()
min()
sum()
median()
n()

DC_Marvel_H %>%
  group_by(Publisher)%>%
  summarize(Altura_Promedio = mean(Height, na.rm = TRUE))

La opción na.rm=TRUE se usa para eliminar los NA que aparecen en esa columna.

7.5.3.7 `mutate()`

El verbo mutate() nos permite crear nuevas variables o agregar columnas al data.frame. De la base de datos infoStats vamos a calcular una nueva variable que relacione Poder y Combate.

infoStats %>%
  mutate(resistencia = Power/Combat)

infoStats %>%
  mutate(resistencia = Power/Combat) %>%
  group_by(Alignment) %>%
  summarize(resistencia_p = mean(resistencia), resistencia_max = max(resistencia), 
            resistencia_min =min(resistencia))

Dentro del verbo mutate se pueden incluir condicionales.

infoStats %>%
  mutate(resistencia = ifelse(Power == 0, 1, Power/Combat)) %>%
  group_by(Alignment) %>%
  summarize(resistencia_p = mean(resistencia), resistencia_max = max(resistencia), 
            resistencia_min =min(resistencia))

7.5.3.8 `transmute()`

El verbo transmute es una combinación de los verbos select y mutate.

infoStats %>%
  transmute(Alignment,  resistencia = Power / Combat)

7.5.3.9 `left_join()`

Existen varios verbos que nos ayudan a unir bases de datos dependiendo de las columnas o filas.

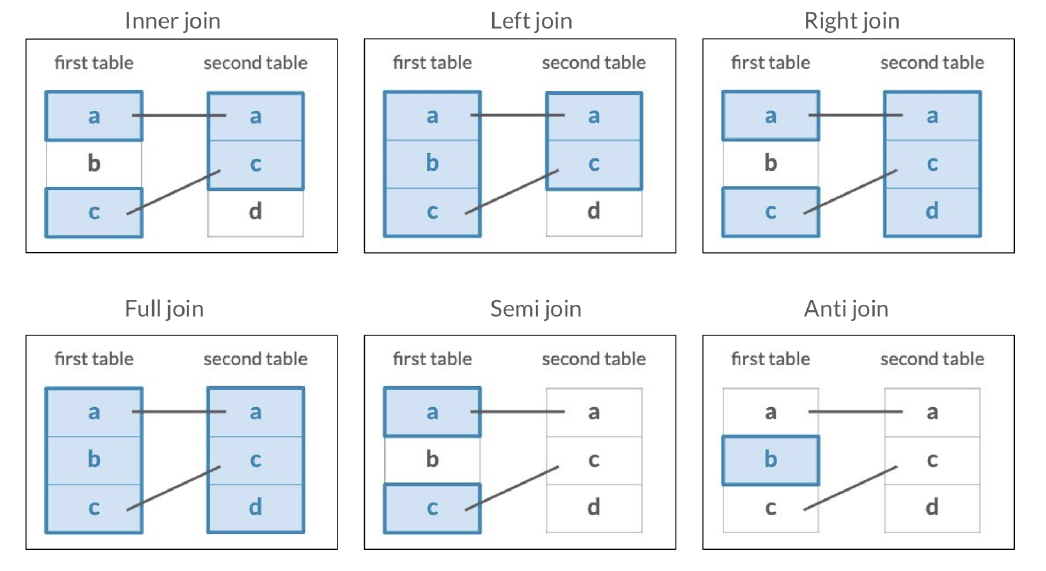Imagen de DATACAMP Vamos a realizar dos uniones, primero vamos a unir la base de datos filtrada DC_Marvel_s con la información de infoStats por Name.

Dc_Marvel_StatsInfo <- left_join(DC_Marvel_s, infoStats, by = "Name")
head(Dc_Marvel_StatsInfo)

Ahora, vamos a unir esta nueva base con la de infoPowers

full_Dc_Marvel <- left_join(Dc_Marvel_StatsInfo, infoPowers, by = "Name")
head(full_Dc_Marvel)

7.5.3.10 Ejercicios

Usa la base de datos full_DC_Marvel. Usa los verbos que acabamos de ver para responder las siguientes preguntas.

¿Cuántos personajes hay?
¿Cuántos personajes hay de cada compañía?
¿Cuántos personajes hay de cada género en cada compañía?
¿Cual es la raza predominante en cada compañía?
¿Cuántos son villanos y cúantos son héroes?
¿Quién es el personaje más fuerte?
¿Quién es el personaje más inteligente?
¿Quién es la mujer más poderosa y malvada? ¿De que compañía es?
¿Quién es el hombre más poderoso y bueno? ¿De que compañía es?
Selecciona a Superman y Iron Man, compara sus Stats, ¿Quién tiene mejor Stats?

Explora los verbos ungroup(), slice_min(), slice_max(). ¿Cómo los podrías usar en la base de datos. Crea un ejemplo con cada uno.

7.6 Análisis exploratorio de bases de datos

Algunas funciones en R para calcular los estadísticos descriptivos:

Descripción	Función en R
Media	`mean()`
Varianza muestral	`var()`
Desviación estándar muestral	`sd()`
Mínimo	`min()`
Máximo	`max()`
Mediana	`median()`
Rango	`range()`
Quantiles	`quantile()`
Rango intercuantil	`IQR()`
Resumen	`summary()`
Moda	`mfv())` del paquete `statip` o `modeest`

Vamos a cargar la base de datos de iris y explorar estás funciones.

data(iris)

7.6.1 Medidas de Tendencia central

Media:

mean(iris$Sepal.Length)

## [1] 5.843333

Mediana:

median(iris$Sepal.Length)

## [1] 5.8

Moda:

# Instalar el paquete statip o modeest primero
library(statip)
mfv(iris$Sepal.Length)

## [1] 5

7.6.2 Medidas de variabilidad

Mínimo:

min(iris$Sepal.Length)

## [1] 4.3

Máximo:

max(iris$Sepal.Length)

## [1] 7.9

Rango:

range(iris$Sepal.Length)

## [1] 4.3 7.9

Quantiles: La función en R para calcular cuantiles es quantile(x, prob = seq(0,1,.25)), se puede especificar el vector de probabilidades con valores $[0,1]$ y el porcentaje, en el ejemplo se estan calculando los cuartiles ya que se especifico 0.25. En el caso de querer los deciles se debería especificar 0.1.

#Cuartiles
quantile(iris$Sepal.Length)

##   0%  25%  50%  75% 100% 
##  4.3  5.1  5.8  6.4  7.9

# Deciles
quantile(iris$Sepal.Length, seq(0,1,0.1))

##   0%  10%  20%  30%  40%  50%  60%  70%  80%  90% 100% 
## 4.30 4.80 5.00 5.27 5.60 5.80 6.10 6.30 6.52 6.90 7.90

Rango intercuantil:

IQR(iris$Sepal.Length)

## [1] 1.3

Varianza: La función en R var() calcula la varianza muestral, es decir:

\[S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2\] Si lo que se quiere es la varianza muestral se puede realizar una función que realice esto.

# Varianza muestral
var(iris$Sepal.Length)

## [1] 0.6856935

# Varianza poblacional

var_pob <- function(x){
  mean((x - mean(x))^2)
}
  
var_pob(iris$Sepal.Length)

## [1] 0.6811222

Para muestras grandes la diferencia entre una y otra es pequeña pero para muestras pequeñas si es significativa la diferencia.

Desviación estándar:

sd(iris$Sepal.Length)

## [1] 0.8280661

sqrt(var(iris$Sepal.Length))

## [1] 0.8280661

7.6.3 Otras funciones

La función summary de R nos da un resumen de estas medidas de tendencia central y variabilidad, se puede usar tanto con una sola variable como con varias.

summary(iris$Sepal.Length)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   4.300   5.100   5.800   5.843   6.400   7.900

summary(iris)

##   Sepal.Length    Sepal.Width     Petal.Length    Petal.Width   
##  Min.   :4.300   Min.   :2.000   Min.   :1.000   Min.   :0.100  
##  1st Qu.:5.100   1st Qu.:2.800   1st Qu.:1.600   1st Qu.:0.300  
##  Median :5.800   Median :3.000   Median :4.350   Median :1.300  
##  Mean   :5.843   Mean   :3.057   Mean   :3.758   Mean   :1.199  
##  3rd Qu.:6.400   3rd Qu.:3.300   3rd Qu.:5.100   3rd Qu.:1.800  
##  Max.   :7.900   Max.   :4.400   Max.   :6.900   Max.   :2.500  
##        Species  
##  setosa    :50  
##  versicolor:50  
##  virginica :50  
##                 
##                 
##

Otra función que es útil en R es la función sapply(), esta nos permite calcular las medidas anteriores para cada columna de la base de datos.

sapply(iris[,1:4], mean)

## Sepal.Length  Sepal.Width Petal.Length  Petal.Width 
##     5.843333     3.057333     3.758000     1.199333

sapply(iris[,1:4], quantile)

##      Sepal.Length Sepal.Width Petal.Length Petal.Width
## 0%            4.3         2.0         1.00         0.1
## 25%           5.1         2.8         1.60         0.3
## 50%           5.8         3.0         4.35         1.3
## 75%           6.4         3.3         5.10         1.8
## 100%          7.9         4.4         6.90         2.5

En el paquete pastecs se encuentra la función stat.desc() la cual nos regresa otras medidas.

# install.packages("pastecs")
library(pastecs)

## 
## Attaching package: 'pastecs'

## The following objects are masked from 'package:dplyr':
## 
##     first, last

## The following object is masked from 'package:tidyr':
## 
##     extract

## The following objects are masked from 'package:data.table':
## 
##     first, last

resumen <- stat.desc(iris[,1:4])

round(resumen, 2)

##              Sepal.Length Sepal.Width Petal.Length Petal.Width
## nbr.val            150.00      150.00       150.00      150.00
## nbr.null             0.00        0.00         0.00        0.00
## nbr.na               0.00        0.00         0.00        0.00
## min                  4.30        2.00         1.00        0.10
## max                  7.90        4.40         6.90        2.50
## range                3.60        2.40         5.90        2.40
## sum                876.50      458.60       563.70      179.90
## median               5.80        3.00         4.35        1.30
## mean                 5.84        3.06         3.76        1.20
## SE.mean              0.07        0.04         0.14        0.06
## CI.mean.0.95         0.13        0.07         0.28        0.12
## var                  0.69        0.19         3.12        0.58
## std.dev              0.83        0.44         1.77        0.76
## coef.var             0.14        0.14         0.47        0.64

Esta función nos regresa el error estándar de la media (SE.mean), el intervalo de confianza para la media al p-valor de default 0.95 (CI.mean.95), el coeficiente de variación (coef.var) que es la desviación estándar entre la media.

En el caso de tener valores faltantes, algunas de las funciones de R regresan error o NA. El tratamiento a estos datos faltantes depende del tipo de valor faltante del que se trate:

MCAR: Missing completely at random, estos datos son cuando la probabilidad de pérdida no depende de lo observado ni de lo no observado, por ejemplo una muestra en un laboratorio accidentalmente se cae y se rompe, la letra del encuestador es ilegible.
MAR: Missing at random, en este caso el mecanismo de pérdida no depende de la información perdida pero si de la observada. Por ejemplo, en un estudio sobre los ingresos y pago de impuestos, las personas que ganan más se podrían negar a revelar sus ingresos. Si se conoce la categoría de pago de impuestos de todos los individuos, la no respuesta acerca del ingreso es MAR, el mecanismo de pérdida depende de la categoría de pago de impuestos(que si es observada), así que la pérdida del dato de ingreso NO depende del valor del ingreso mismo (que no se observo).
MNAR: Missing not at random, el mecanismo de pérdida no es ignorable si los valores perdidos dependen de los valores no observados. Por ejemplo, cuantas ayudas recibe la familia del gobierno, tienden a no contestar los que tienen más ayudas.

El tratamiento que se les debe dar a los datos depende de estas categorías, algunos de ellos son imputación simple, imputación múltiple, borrar casos, colocar la media en los valores faltantes, hot deck(se rellena con otro parecido), predicción, etc. En todos los casos uno puede sobreestimar los parámetros y nos puede llevar a tener resultados sesgados.

Si queremos digamos borrar los casos, en R especificamos na.rm= TRUE en las funciones.

mean(iris$Sepal.Length, na.rm = TRUE)

## [1] 5.843333

Tablas de frecuencia

Vamos a cargar la base de datos HairEyeColor que contiene datos de sexo, color de cabello y ojos de 592 estudiantes.

datos <- as.data.frame(HairEyeColor)
hair_eye_color <- datos[rep(row.names(datos), datos$Freq), 1:3]

rownames(hair_eye_color) <- 1: nrow(hair_eye_color)

head(hair_eye_color)

##    Hair   Eye  Sex
## 1 Black Brown Male
## 2 Black Brown Male
## 3 Black Brown Male
## 4 Black Brown Male
## 5 Black Brown Male
## 6 Black Brown Male

hair_col <- hair_eye_color$Hair
eye_col <- hair_eye_color$Eye

table(hair_col)

## hair_col
## Black Brown   Red Blond 
##   108   286    71   127

table(eye_col)

## eye_col
## Brown  Blue Hazel Green 
##   220   215    93    64

library(ggplot2)
df_hair <- as.data.frame(table(hair_col))

cl <- c("black", "brown", "red", "gold")
ggplot(df_hair, aes(x=hair_col, y=  Freq, fill= hair_col)) +
  geom_bar(stat = "identity")+
  scale_fill_manual(values=cl)+
  labs(title = "Color de cabello de 592 estudiantes",
       subtitle = "HairEyeCol data set",
       x = "Color de cabello",
       y = "Cantidad de estudiantes",
       caption = "Datos: data(HairEyeCol)`",
       fill = "Color de Cabello")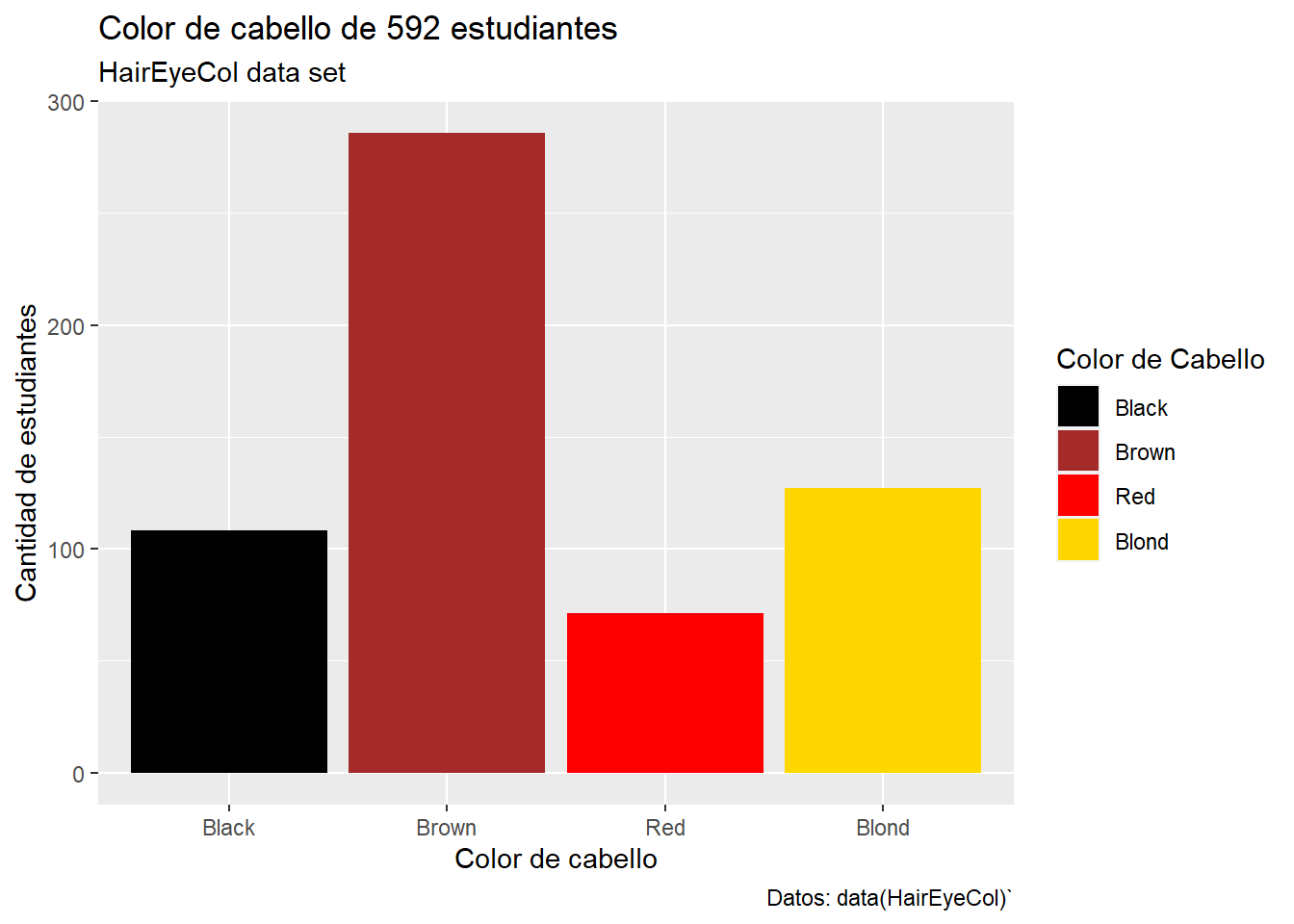

Tabla de contingencia para dos variables:

datos2 <- table(hair_col, eye_col)
datos2

##         eye_col
## hair_col Brown Blue Hazel Green
##    Black    68   20    15     5
##    Brown   119   84    54    29
##    Red      26   17    14    14
##    Blond     7   94    10    16

df_hair_eye <- as.data.frame(datos2)

p <- ggplot(df_hair_eye, aes(x=hair_col, y=  Freq, fill=eye_col)) +
  geom_bar(stat = "identity") +
  labs(title = "Color de cabello de 592 estudiantes",
       subtitle = "HairEyeCol data set",
       x = "Color de cabello",
       y = "Cantidad de estudiantes",
       caption = "Datos: data(HairEyeCol)`",
       fill = "Color de Cabello")
p + scale_fill_manual(values = c("brown","blue", "gold", "green"))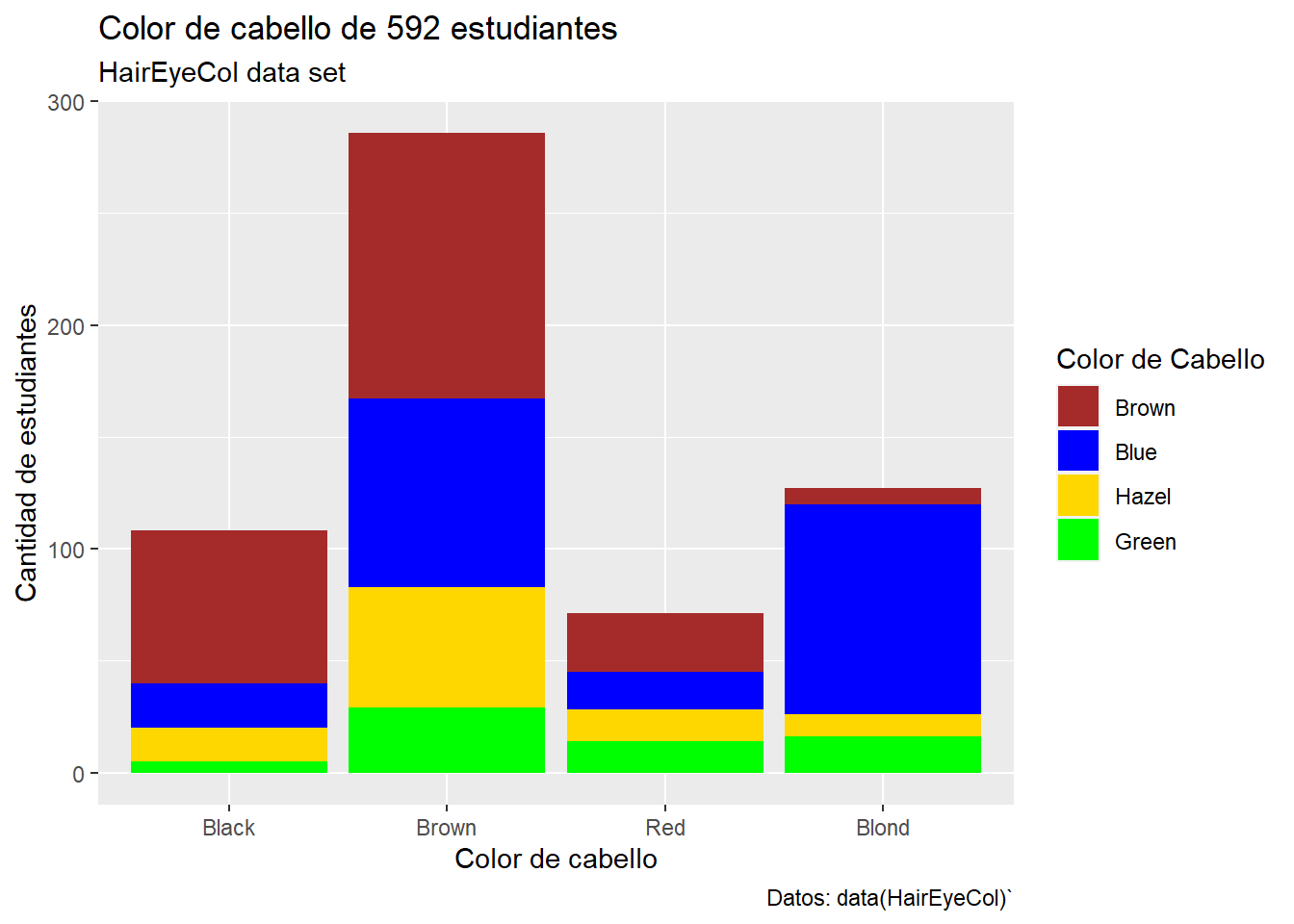

p2 <- ggplot(df_hair_eye, aes(x=hair_col, y=  Freq, fill=eye_col)) +
  geom_bar(stat = "identity", position = position_dodge()) +
  labs(title = "Color de cabello de 592 estudiantes",
       subtitle = "HairEyeCol data set",
       x = "Color de cabello",
       y = "Cantidad de estudiantes",
       caption = "Datos: data(HairEyeCol)`",
       fill = "Color de Cabello")
p2 + scale_fill_manual(values = c("brown","blue", "gold", "green"))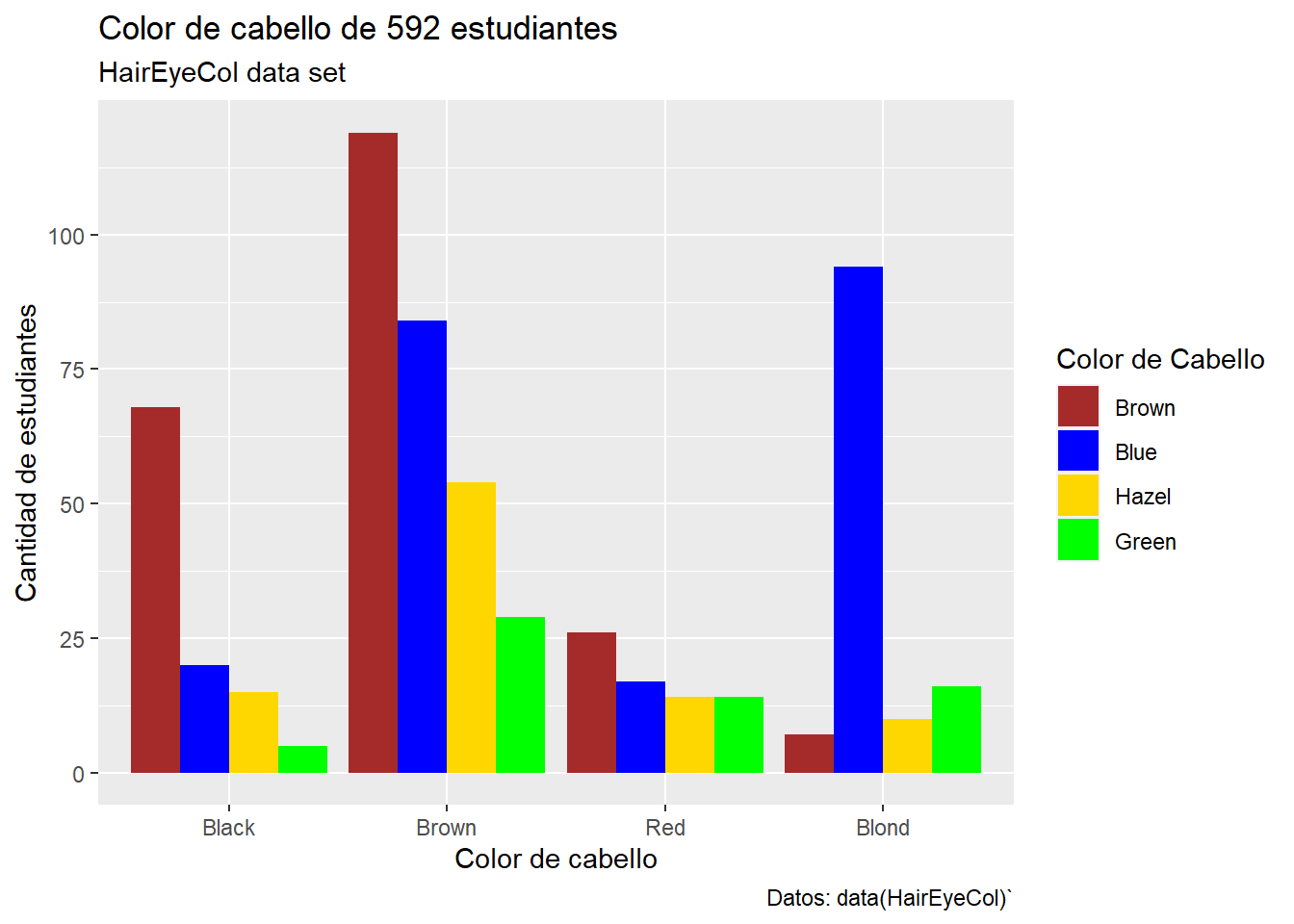

7.6.4 Ejercicios

Analiza la Tabla siguiente (Consumer Report Buying Guide 2002) que contiene algunos datos (precio, calidad de sonido, caseteras, etc.) de algunas marcas de minicomponentes y responde las siguientes preguntas:

Marca y modelo	Precio $(\$)$	Calidad de sonido	Capacidad para CD	Sintonización FM	Caseteras
Aiwa NSX-AJ800	250	Buena	3	Regular	2
JVC FS-SD1000	500	Buena	1	Muy buena	0
JVC MX-G50	200	Muy buena	3	Excelente	2
Panasonic SC-PM11	170	Regular	5	Muy buena	1
RCA RS 1283	170	Buena	3	Mala	0
Sharp CD-BA2600	150	Buena	3	Buena	2
Sony CHC-CL1	300	Muy buena	3	Muy buena	1
Sony MHC-NX1	500	Buena	5	Excelente	2
Yamaha GX-505	400	Muy buena	3	Excelente	1
Yamaha MCR-E100	500	Muy buena	1	Excelente	0

¿Cuántos elementos contiene este conjunto de datos y cuál es la población?
Calcula el precio promedio en la muestra.
Con el resultado anterior, estima el precio promedio para la población.
¿Cuántas variables hay en este conjunto de datos? Clasifícalas en cuantitativas y cualitativas
¿Qué porcentaje de los minicomponentes tienen una sintonización de FM buena o excelente?

Un biólogo que estudia cierta reserva ecológica está interesado en analizar su temperatura. A continuación se presenta las temperaturas promedio observadas de 40 días elegidos aleatoriamente.

Temperaturas observadas (en °C)

14.4, 17.5, 31.1, 28.0, 17.2, 34.1, 21.8, 18.1, 19.0, 25.0, 21.1, 27.8, 28.7, 21.1, 26.1, 33.6, 29.0, 20.2, 31.3, 25.1,31.6, 25.2, 19.0, 26.3, 25.5, 16.9, 20.9, 23.2, 26.6, 32.0, 28.2, 22.3, 29.2, 22.6, 29.6, 16.6, 22.7, 23.9, 26.3, 24.6

Construye la distribución de frecuencias individuales y acumuladas (absolutas y relativas) de la temperatura de la reserva ecológica considerando 5 clases de igual longitud sobre el intervalo [10, 40].
Construye el histograma de frecuencias relativas de la temperatura de la reserva ecológica considerando las clases del inciso anterior.
Construye la ojiva de la temperatura de la reserva ecológica considerando las clases del inciso 1. Consultar liga para la realización de la ojiva.
Calcula la media, mediana y moda de los datos.

A continuación se presenta el diagrama de tallo y hojas del contenido de cloro (en mililitros) de una muestra de 20 botes de un lote de producción.

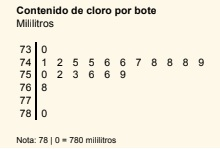
Figure 7.1: Contenido de cloro

Calcula el percentil 0.05 de la distribución del contenido de cloro por bote.
Calcula el cuantil 0.05 de la distribución del contenido de cloro por bote.
Calcula los cuartiles de la distribución del contenido de cloro por bote.
Calcula los coeficientes de asimetría y curtosis.

Nota: El coeficiente de asimetría mide la proximidad de los datos a su media. Cuando mayor sea la suma $\sum_{i=1}^n(x_i - \bar{x})^3$ mayor será la asimetría. Para una colección de datos $x_1,x_2,...,x_n$ con media $\bar{x}$ y desviación estándar $s$, el coeficiente de asimetría se calcula como:

\[k=\frac{1}{s^3}\left( \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})^3\right)\]

La curtosis mide que tan puntiaguda o achatada es la distribución de los datos, indica la cantidad de datos que hay cercanos a la media, para una colección de datos $x_1,x_2,...,x_n$ con media $\bar{x}$ y desviación estándar $s$ esta dado por el número: \[k=\frac{1}{s^4}\left( \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})^4\right)\]

Los siguientes tiempos (cronometrados en segundos) fueron registrados por una muestra de 5 corredores durante una carrera de 100 metros planos: 9.82, 9.91, 9.94, 9.95 y 9.98.

Calcula la amplitud o rango de los tiempos observados.
Calcula la varianza de los tiempos observados.
Calcula la desviación estándar de los tiempos observados.
Calcula el coeficiente de variación de los tiempos observados. Interprete.

La Figura siguiente muestra una tabla que contiene el número de accidentes de tráfico en una muestra de estados (de Estados Unidos), entre 2007 y 2008. Grafica un scatter plot y encuentra el coeficiente de correlación muestral para los pares de datos.

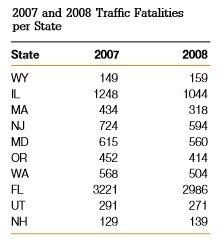
Figure 7.2: Datos de Accidentes de Tráfico

En cada uno de los siguientes casos determina qué tipo de escala de medición es la más adecuada para cada una de ellas:

El Director de Mercadotecnia de una Editorial desea conocer la opinión del público respecto a las secciones (política, finanzas, deportes, cultura, ciudad,cocina) que debe incluir una nueva revista.
El Gobierno de la Ciudad de México desea conocer si los habitantes del Distrito Federal están a favor o en contra de la construcción de un nuevo distribuidor vial.
Con la finalidad de establecer estándares de calidad, una cadena de restaurantes desea conocer la calificación (excelente, bueno, regular, malo) que dan sus clientes a los meseros.
El Director de Operaciones de Teléfonos de México (TELMEX), desea conocer el número de llamadas de larga distancia que se realizan por mes.
La Comisión Nacional de Aguas quiere estimar el consumo promedio de agua por familia en cada uno de los municipios del Estado de México.
Un Biólogo desea determinar la temperatura que debe tener un estanque para tener cierta especie de ballenas en cautiverio.

7.7 Reportes con RMarkdown

Link a github con tutorial