Sección 8 Estadística multivariada
8.1 Correlaciones y distancias
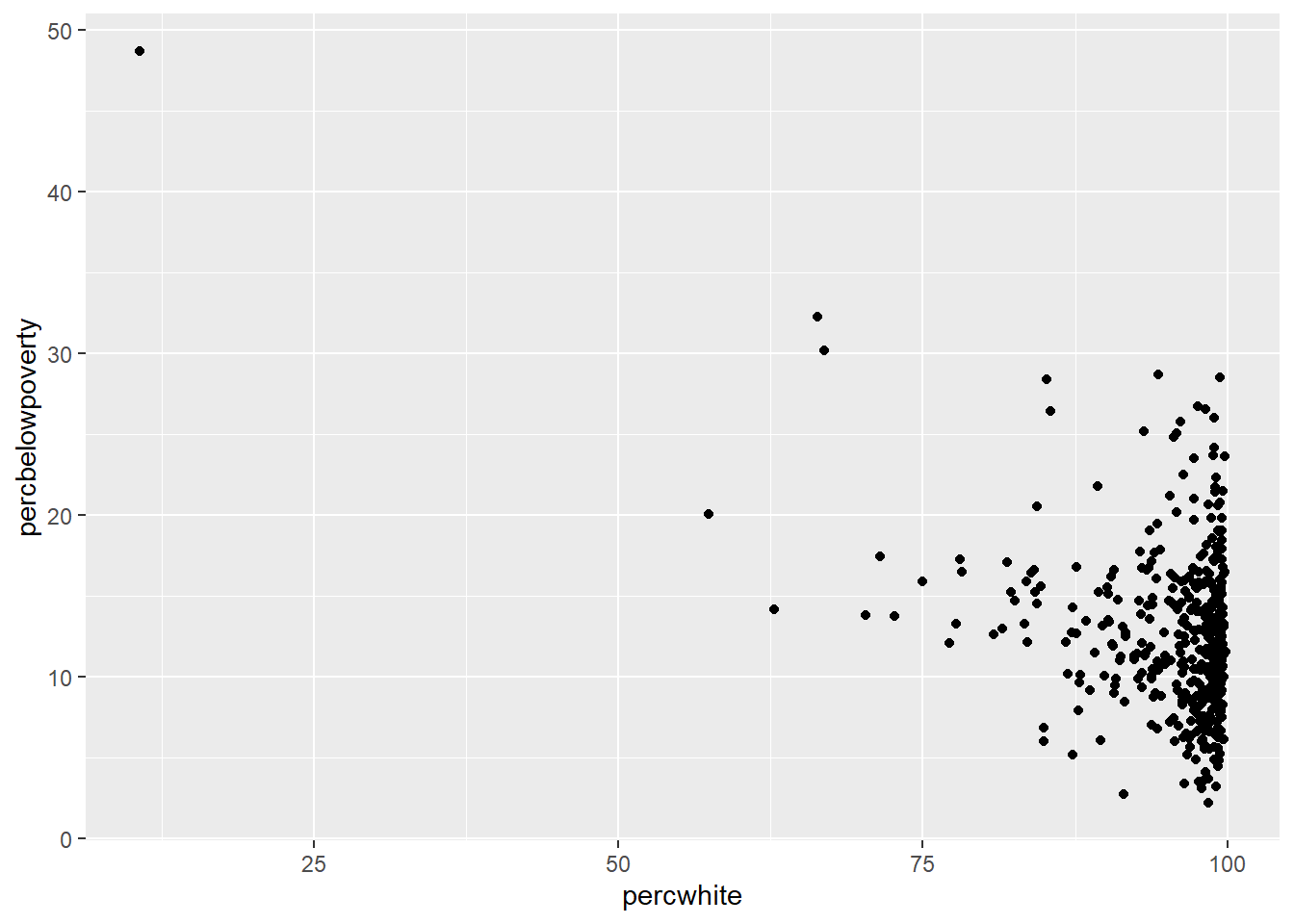
Con los siguientes dos paquetes se pueden realizar los plots de las matrices de correlaciones y distancias.
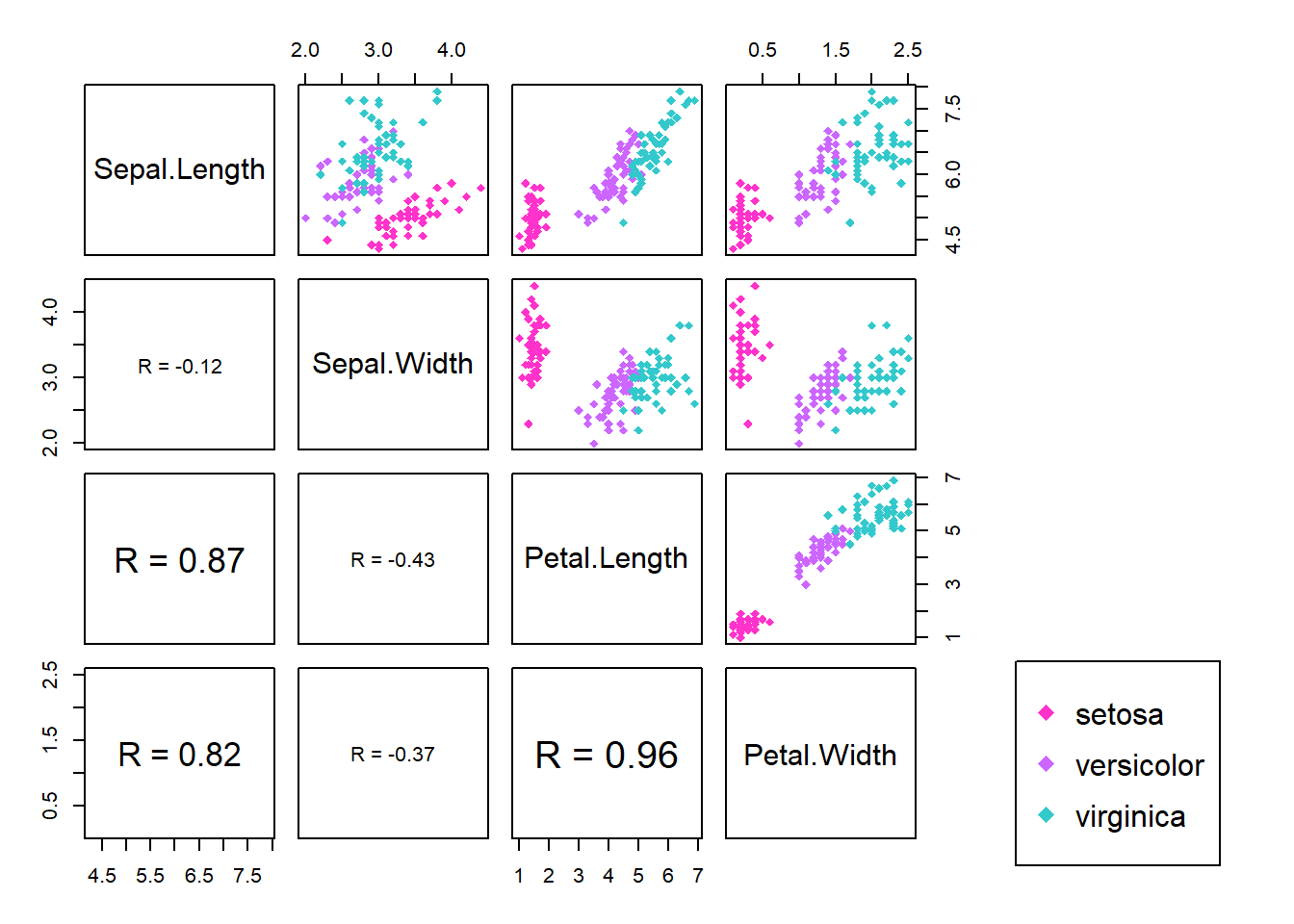
cor.mat_all <- cor(data.matrix(iris[,-5]), use="complete.obs")
corplot_all <- corrplot(cor.mat_all, method="shade", tl.col = "black", tl.srt = 45,
number.cex = 0.4, addCoef.col = "black",order = "AOE",type = "upper",addshade = "all", diag = F)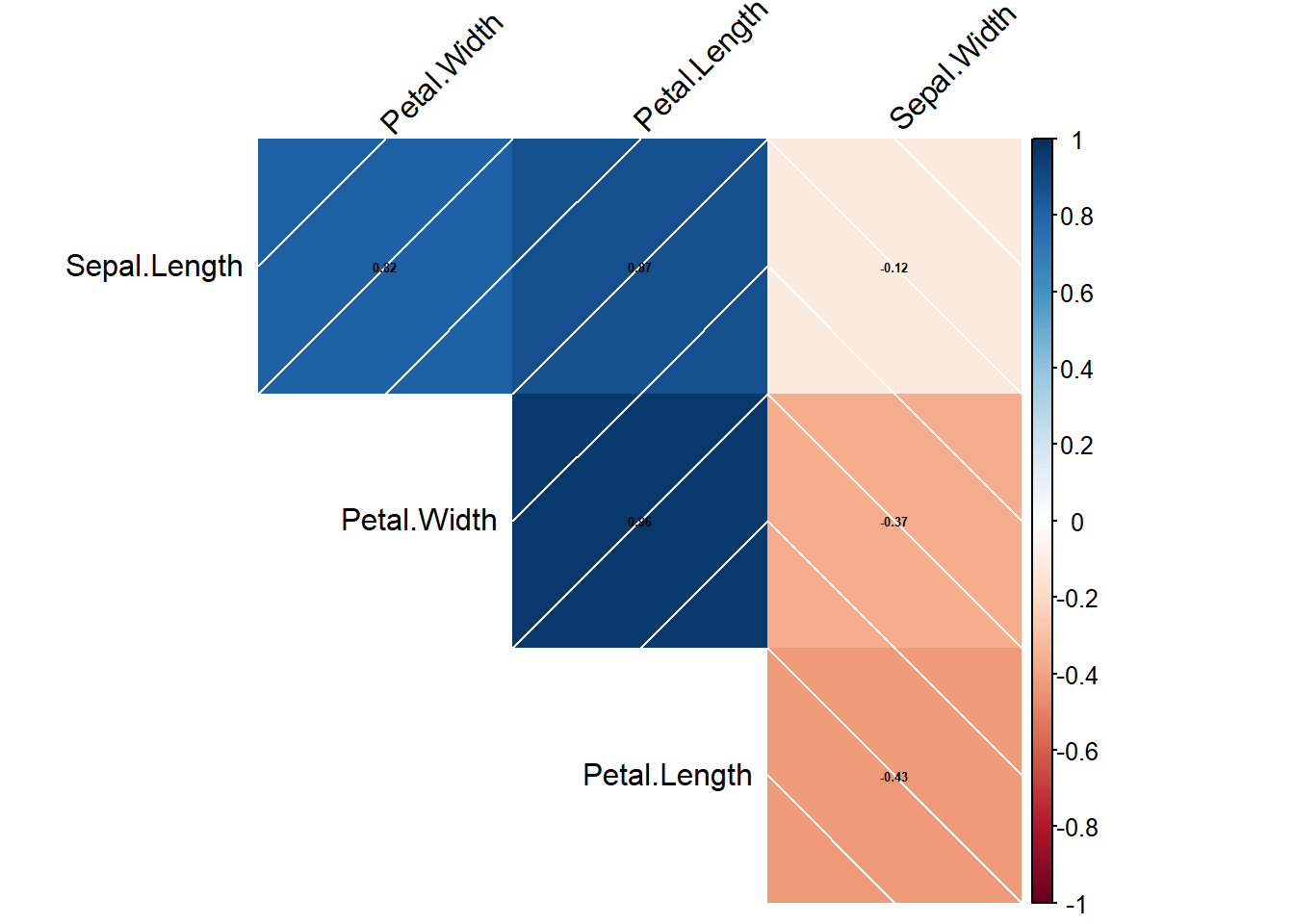
8.2 Plots Multivariados
8.2.1 Caritas de Chernoff
Instala el paquete aplpack y carga la base de datos iris.
faces(iris[c(1,51,101),1:4],
nrow.plot = 1,
ncol.plot = 3,
main = "La primer flor de cada especie", print.info = TRUE)
## effect of variables:
## modified item Var
## "height of face " "Sepal.Length"
## "width of face " "Sepal.Width"
## "structure of face" "Petal.Length"
## "height of mouth " "Petal.Width"
## "width of mouth " "Sepal.Length"
## "smiling " "Sepal.Width"
## "height of eyes " "Petal.Length"
## "width of eyes " "Petal.Width"
## "height of hair " "Sepal.Length"
## "width of hair " "Sepal.Width"
## "style of hair " "Petal.Length"
## "height of nose " "Petal.Width"
## "width of nose " "Sepal.Length"
## "width of ear " "Sepal.Width"
## "height of ear " "Petal.Length"Para los elementos de color de las caras, los colores son encontrados al promediar los conjuntos de variables: (7,8)-eyes:iris, (1,2,3)-lips, (14,15)-ears, (12,13)-nose, (9,10,11)-hair, (1,2)-face (From ?faces).
Grafiquemos las primeras 10 flores de cada especie:
faces(iris[c(1:10,51:60,101:110),1:4],
nrow.plot = 3,
ncol.plot = 10,
main = "Las primeras 10 flores de cada especie", print.info = FALSE)
Ahora grafiquemos las primeras 5:
faces(iris[c(1:5,51:55,101:105),1:4],
nrow.plot = 3,
ncol.plot = 5,
main = "Las primeras 5 flores de cada especie", print.info = FALSE)
Aquí podemos notar que la carita 54 es muy diferente a las demás de su especie- La carita 102 se parece más a la de la especie 55 que a las suyas. El pelo de la primera especie es muy diferente a los de las otras especies.
Es muy “fácil” hacer grupos a ojo.
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 7.9 4.4 6.9 2.5## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 4.3 2.0 1.0 0.1chico<-c(4,2,1,.05) # Valores más chicos de las 4 variables.
grande<-c(8,5,7,3) # Valores más grandes de las 4 variables.
faces(rbind(iris[c(1:10,51:60,101:110),1:4],chico,grande), nrow.plot=5, ncol.plot=10,main="Primeros 10 de cada especie + chico + grande" )
## effect of variables:
## modified item Var
## "height of face " "Sepal.Length"
## "width of face " "Sepal.Width"
## "structure of face" "Petal.Length"
## "height of mouth " "Petal.Width"
## "width of mouth " "Sepal.Length"
## "smiling " "Sepal.Width"
## "height of eyes " "Petal.Length"
## "width of eyes " "Petal.Width"
## "height of hair " "Sepal.Length"
## "width of hair " "Sepal.Width"
## "style of hair " "Petal.Length"
## "height of nose " "Petal.Width"
## "width of nose " "Sepal.Length"
## "width of ear " "Sepal.Width"
## "height of ear " "Petal.Length"Ejercicio: Explora el siguiente plot, ¿porqué sonrisas?.
faces(cbind(iris[1:15,1:4],rep(1:5,rep(3,1)), rep(c(2,4,6),rep(5,3))),
nrow.plot = 3,
ncol.plot = 5,
main = "¿Sonrisas?", print.info = FALSE)
Con las caritas de Chernoff es mejor la representación o visualización si se tienen pocos datos y se pueden representar hasta 15 variables.
8.2.2 Curvas de Andrew
Instala y carga el paquete Andrews.
library(andrews)
par(mfrow=c(2,2))
andrews(iris, type = 1, clr = 5, ymax = 3, main = "Curva tipo 1")
andrews(iris, type = 2, clr = 5, ymax = 3, main = "Curva tipo 2")
andrews(iris, type = 3, clr = 5, ymax = 3, main = "Curva tipo 3")
andrews(iris, type = 4, clr = 5, ymax = 3, main = "Curva tipo 4")
Podemos observar que las especies de color rojo se separan más de las otras dos en casi todos los casos. Hay intersecciones en las curvas.
Ejercicio: Carga las bases de datos mtcars y ChickWeight y explora sus curvas de Andrews.
8.2.3 Gráficos de Paralelas
En el eje Y podemos ver todas las variables. Los cruces reflejan correlaciones negativas entre las variables.
parallelplot(~mtcars[,c(1,6,7,3,4,5)],col=as.numeric(mtcars$cyl)-3,main="Plot de paralelas por Cilindros" )
En este plot se pueden ver los grupos por colores, los que pesan poco tienen un mayor rendimiento. Cuando no hay cruces reflejan correlación positiva.
Si calculamos la matriz de correlaciones, podemos ver que las variables con correlación negativa se reflejan aqui también.
## mpg disp hp drat
## mpg 1.00 -0.85 -0.78 0.68
## disp -0.85 1.00 0.79 -0.71
## hp -0.78 0.79 1.00 -0.45
## drat 0.68 -0.71 -0.45 1.00Estos graficos también dependen del orden de las variables.
Ejercicio: realiza dos plots de paralelas de la base de datos iris, uno divido por especie y otro donde el color vaya a la variable especie. ¿Qué puedes decir al respecto?
8.2.4 Estrellas
palette(rainbow(12, s = 0.6, v = 0.75))
stars(mtcars[, 1:7], len = 0.8, key.loc = c(12, 1.5),
main = "Motor Trend Cars", draw.segments = TRUE)
También se puede realizar un plot de radar.
stars(mtcars[, 1:7], locations = c(0, 0), radius = FALSE,
key.loc = c(0, 0), main = "Motor Trend Cars", lty = 2)
Ejercicio: Crea los plots de estrellas de la base de datos iris. ¿Qué puedes inferir de ellos?
8.3 Clusters
Existen varias familias de métodos de agrupamiento disponibles en la literatura (Legendre y Legendre 2012): algoritmos secuenciales o algoritmos simultáneos, aglomerativos o divisivos, monotéticos o politéticos, métodos jerárquicos o métodos no jerárquicos, métodos probabilísticos frente a métodos no probabilísticos.
Los métodos jerárquicos aglomerativos, dan origen a un gráfico llamado dendrogramas. Estos métodos son iterativos y en cada paso debe recalcularse la matriz de distancias, lo cual para bases de datos muy grandes suele consumir mucho tiempo de cómputo.
En este capítulo se ilustran varios métodos de clustering diferentes, incluyendo:
- Single linkage agglomerative clustering o método de la liga sencilla o del vecino más cercano.
- Complete linkage agglomerative clustering o método de la liga completa o del vecino más lejano.
- Average linkage agglomerative clustering o métdod de la liga promedio.
- Ward’s minimum variance clustering o método Ward.
8.3.1 Clustering aglomerativo de la liga sencilla
“Aglomerar” significa reunir en un clúster; la agrupación aglomerativa de la liga sencilla también se denomina clasificación de vecinos más cercanos. En cada paso, la agrupación combina dos muestras que contienen las distancias más cortas entre pares (o la mayor similitud), es decir, se toma la mínima de todas las posibles distancias entre los objetos que pertenecen a distintos conglomerados:
\[d_{AB}=\min_{i\in A, j\in B} (d_{ij}).\]

El resultado de la agrupación puede visualizarse como un dendrograma. El inconveniente del dendrograma resultante de un clustering de liga sencilla a menudo muestra el encadenamiento de las muestras. Los clústeres formados se ven forzados a unirse debido a que los elementos individuales están cerca unos de otros, mientras que muchos elementos de cada clúster pueden estar muy alejados entre sí. Otro inconveniente relevante del clustering de la liga sencilla es que podría ser difícil de interpretar en términos de particiones de los datos. Es una desventaja real del clustering de la liga sencilla porque estamos interesados en las particiones de los datos. Este método se tiende a desempeñar bien cuando hay grupos de forma elongada, conocidos como tipo cadena.
Vamos a realizar los ejemplos con la siguiente base de datos.
A <- c(0,4,15,6,2,9)
B <- c(4,0,5,7,6,10)
C <- c(15,5,0,9,3,15)
D <- c(6,7,9,0,10,3)
E <- c(2,6,3,10,0,2)
F <- c(9,10,15,3,2,0)
df <- data.frame(A,B,C,D,E,F, row.names = c("A","B","C","D","E","F"))
df %>% knitr::kable(format = "html")| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 0 | 4 | 15 | 6 | 2 | 9 |
| B | 4 | 0 | 5 | 7 | 6 | 10 |
| C | 15 | 5 | 0 | 9 | 3 | 15 |
| D | 6 | 7 | 9 | 0 | 10 | 3 |
| E | 2 | 6 | 3 | 10 | 0 | 2 |
| F | 9 | 10 | 15 | 3 | 2 | 0 |
Figure 8.1: Cluster con el método single.
8.3.2 Clustering aglomerativo de la liga completa
El clustering de la liga completa también se conoce como clustering del vecino más lejano. Permite que que una muestra (o un grupo) se aglomere con otra muestra (o grupo) sólo a la distancia más lejana entre sí. Así, todos los miembros de ambos grupos están vinculados.
\[d_{AB}=\max_{i\in A, j\in B} (d_{ij}).\]

La agrupación de la liga completa evita el inconveniente de encadenar las muestras por el método de la liga simple. El encadenamiento completo tiende a encontrar muchos pequeños grupos separados. Este método se desempeña bien cuando los conglomerados son de forma circular.
Figure 8.2: Cluster con el método complete.
8.3.3 Clustering aglomerativo de la liga promedio
La agrupación de liga promedio permite agrupar una muestra en un clúster en la media de las distancias entre esta muestra y todos los miembros del clúster. Los dos clusters se unen a la media de las distancias entre todos los miembros de un clúster y todos los miembros del otro.
\[d_{AB}=\frac{1}{n_An_B} \sum_{i\in A} \sum_{j\in B} (\ d_{ij}\ ).\]
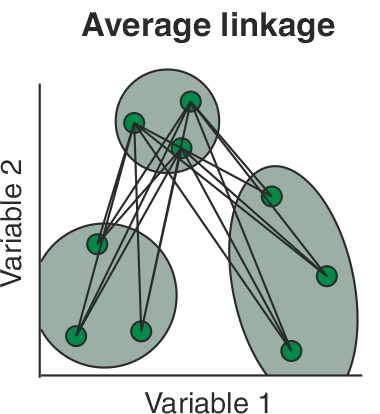
El clúster resultante del dendrograma tiene un aspecto intermedio entre una agrupación de enlace simple y una completa.
Figure 8.3: Cluster con el método average.
8.3.4 Agrupación de varianza mínima de Ward
La agrupación de varianza mínima de Ward (también conocida como agrupación de Ward) presentada originalmente por Ward (1963) se basa en el criterio del modelo lineal de mínimos cuadrados. Este método método minimiza las sumas de las distancias al cuadrado (es decir, el error al cuadrado de ANOVA) entre las muestras. Básicamente, considera el análisis de conglomerados como un análisis de la varianza, en lugar de utilizar métricas de distancia o medidas de asociación. Este método es más apropiado para las variables cuantitativas, y no variables binarias. El clustering de Ward se implementa mediante la búsqueda del par de clusters en cada paso que conduce al mínimo incremento de la varianza total dentro del cluster después de la fusión. Este incremento es una distancia cuadrada ponderada entre los centros de los clusters. Aunque las distancias iniciales de los clusters se definen como la distancia euclidiana al cuadrado entre puntos en el clustering de Ward, otros métodos de distancia pueden producir resultados significativos.
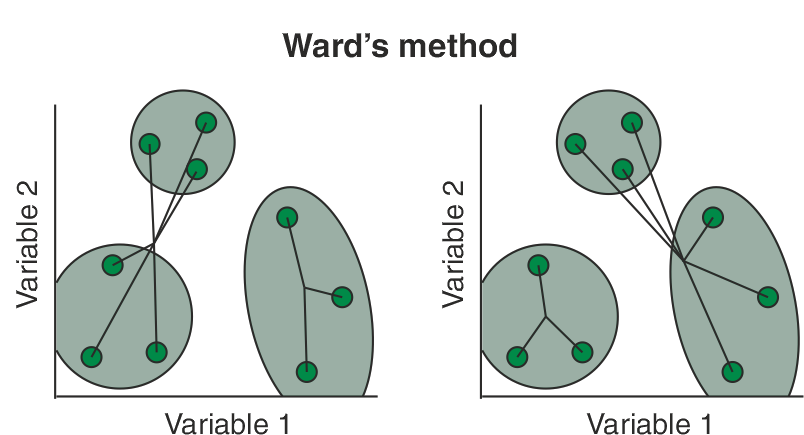
Figure 8.4: Cluster con el método Ward.
# Correrlo en consola para visualizarlo mejor
par (mfrow = c(2,2))
plot(cluster_single)
plot(cluster_complete)
plot(cluster_average)
plot(cluster_ward)
Figure 8.5: Comparación de los clusters con los 4 métodos.
¿Qué puedes decir al respecto si comparas el desempeño de estos 4 métodos?
8.3.5 Mismos gráficos usando el paquete factoextra
Figure 8.6: Heatmap de la matriz de distancias
set.seed(12345)
hc_single <- hclust(d=dist, method = "single")
hc_average <- hclust(d=dist, method = "average")
hc_complete <- hclust(d=dist, method = "complete")
hc_ward <- hclust(d=dist, method = "ward.D2")
## Otros dos métodos
hc_median <- hclust(d=dist, method = "median")
hc_centroid <- hclust(d=dist, method = "centroid")fviz_dend(x = hc_single, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",
horiz = TRUE)+
geom_hline(yintercept = 2.5, linetype = "dashed")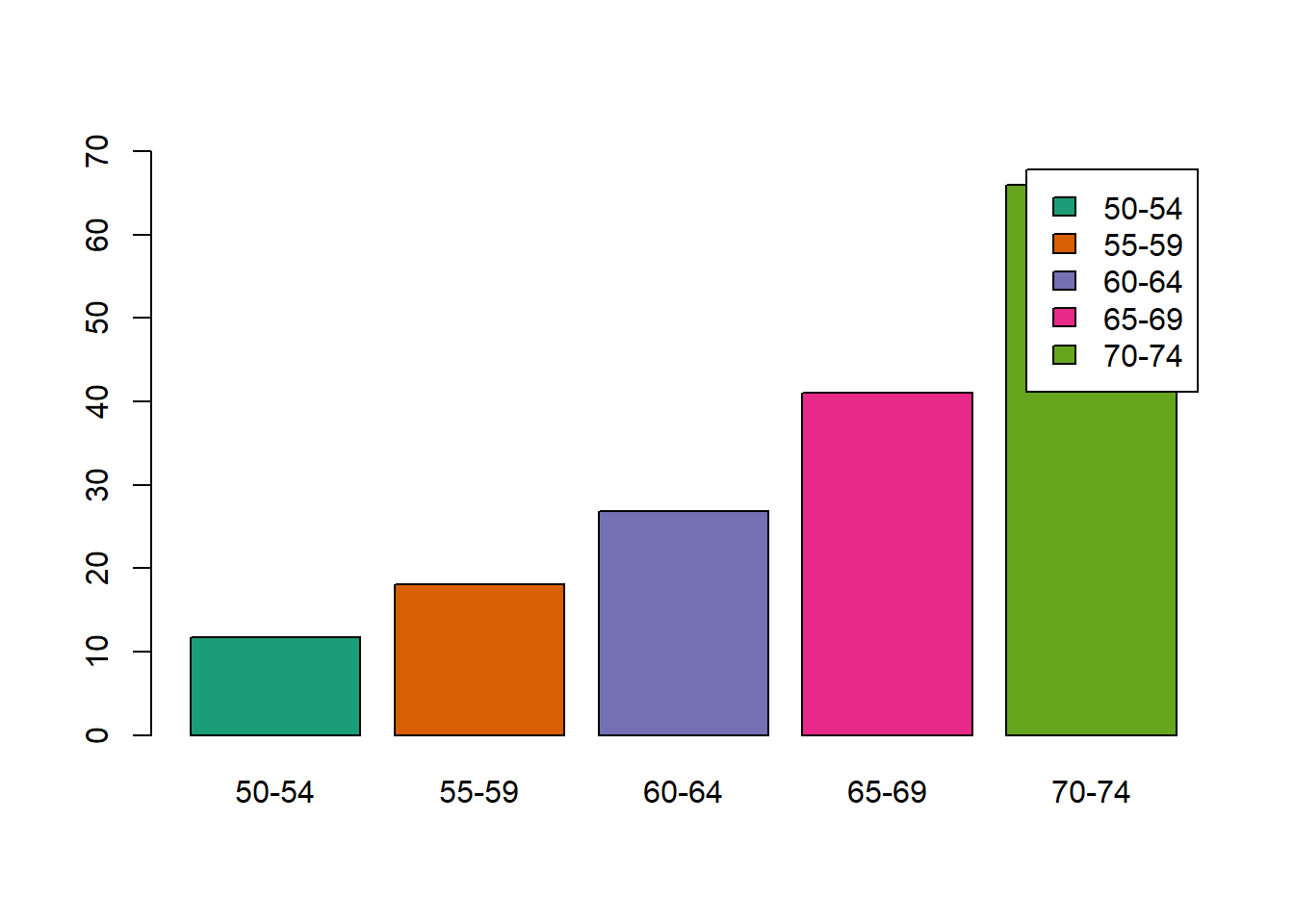
Figure 8.7: Cluster con el método de la liga más sencilla.
fviz_dend(x = hc_complete, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",horiz = TRUE)+
geom_hline(yintercept = 6, linetype = "dashed")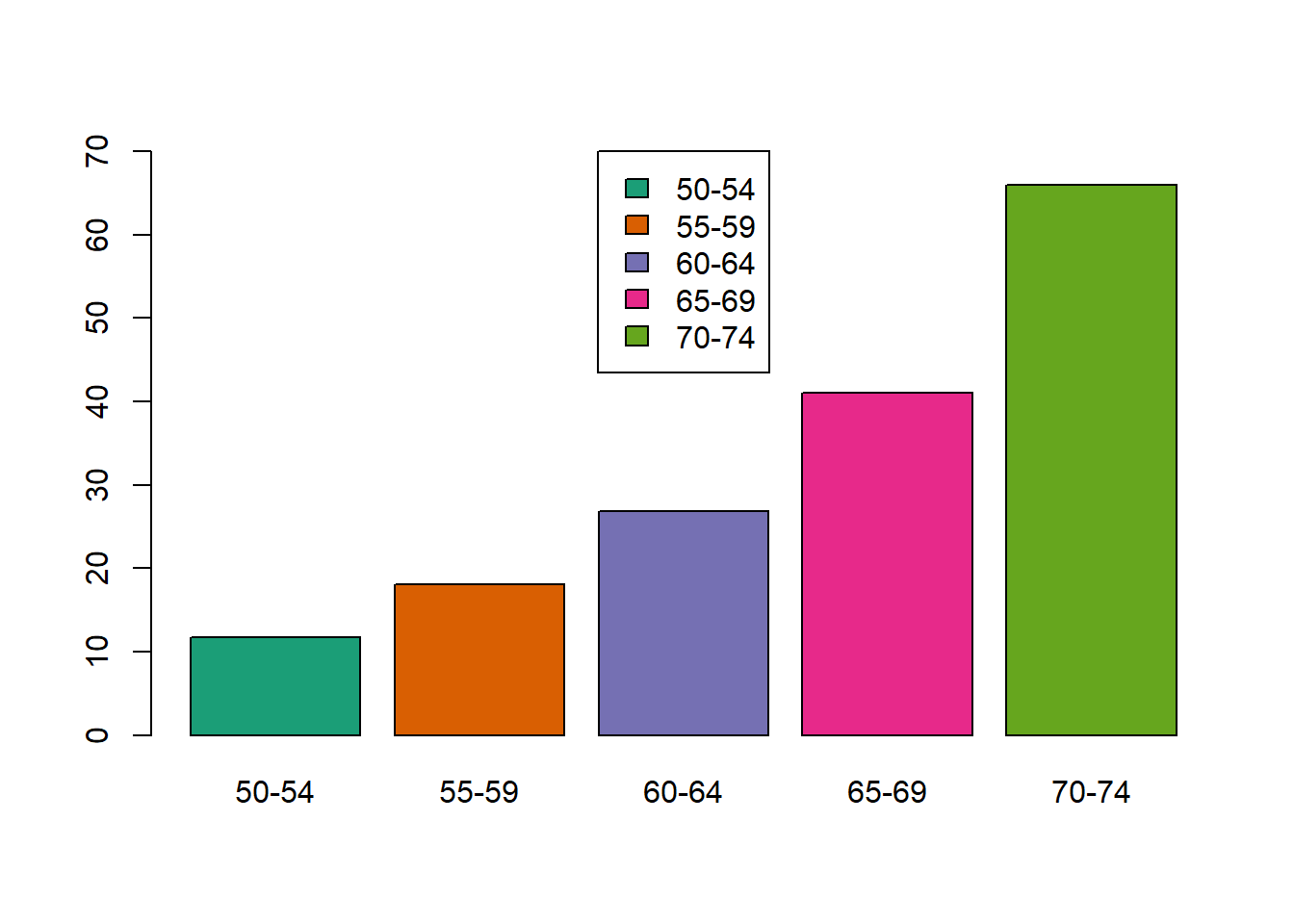
Figure 8.8: Cluster con el método de la liga completa.
fviz_dend(x = hc_average, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",
horiz = TRUE) +
geom_hline(yintercept = 4, linetype = "dashed") 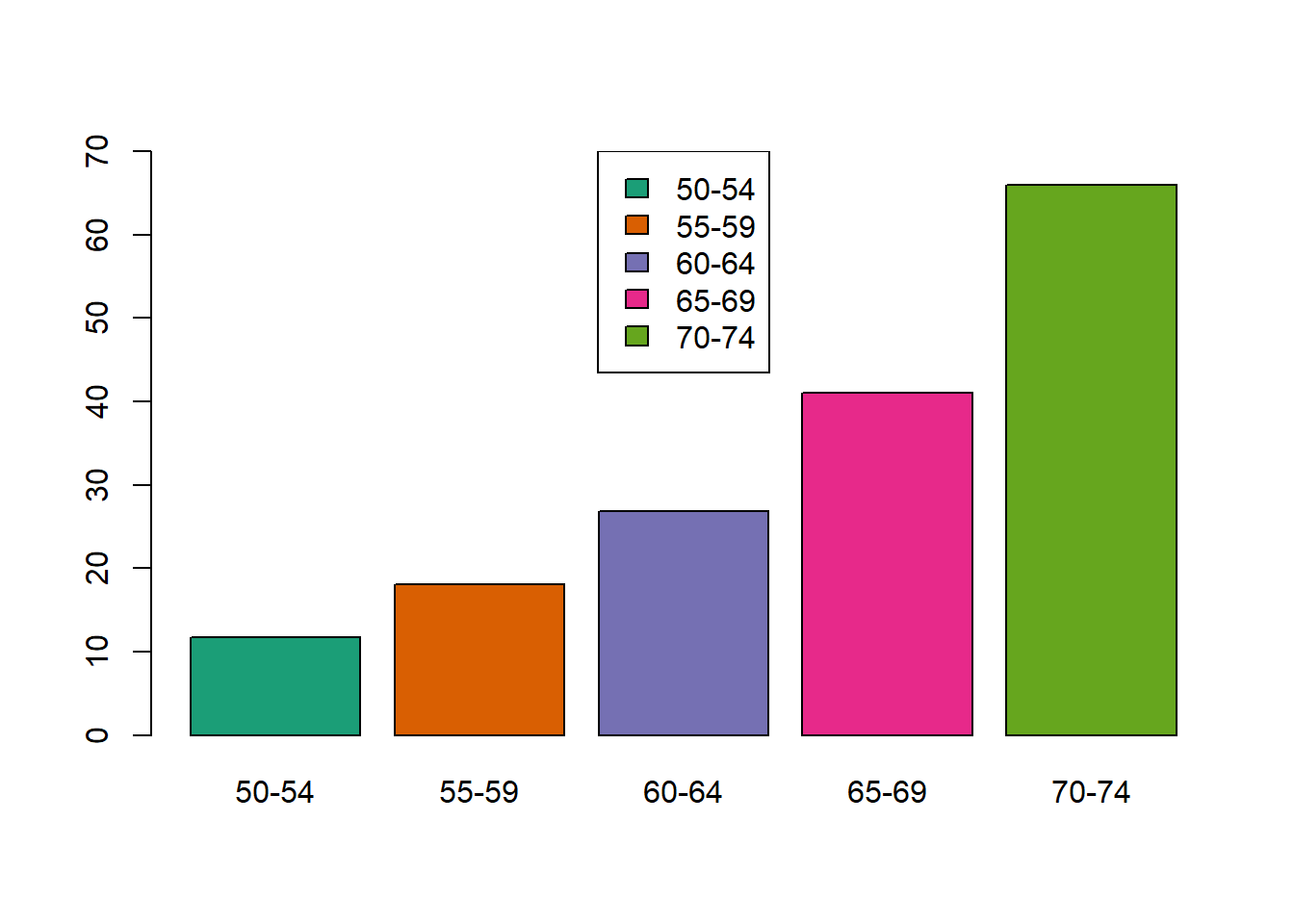
Figure 8.9: Cluster con el método del promedio.
fviz_dend(x = hc_ward, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",
horiz = TRUE)+
geom_hline(yintercept = 6, linetype = "dashed")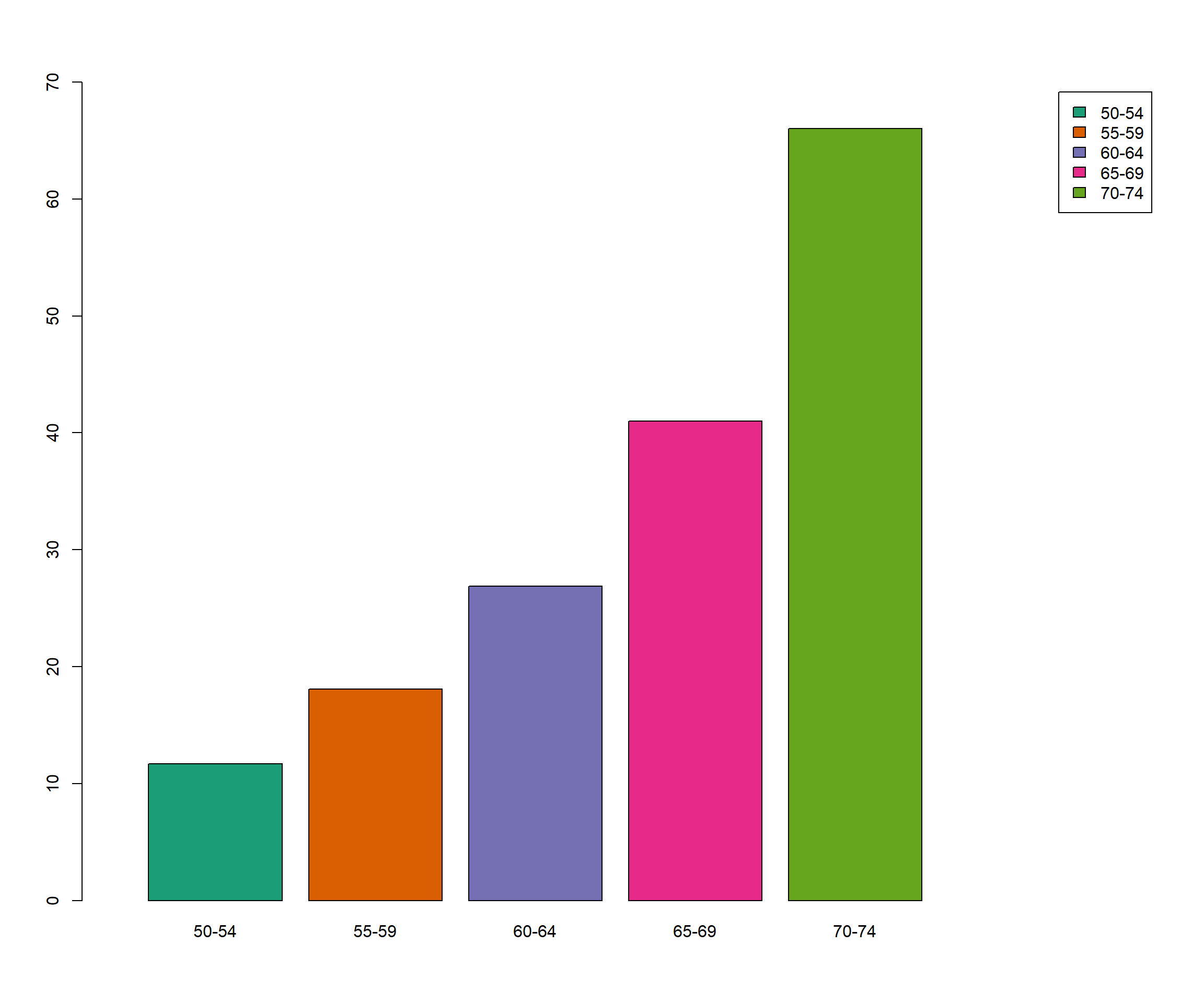
Figure 8.10: Cluster con el método Ward.
fviz_dend(x = hc_median, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",
horiz = TRUE)+
geom_hline(yintercept = 5, linetype = "dashed")
Figure 8.11: Cluster con el método mediana.
fviz_dend(x = hc_centroid, k=3,
cex = 0.7,
main = "",
xlab = "Samples",
ylab = "Distance",
sub = "",
horiz = TRUE)+
geom_hline(yintercept = 4.7, linetype = "dashed")
Figure 8.12: Cluster con el método del centroide.
8.3.6 Número óptimo de clústers
Para evaluar cual dendrograma reflejaba mejor las distancias originales entre las observaciones, calculamos el coeficiente de correlación entre las distancias cofenéticas del dendrograma y la matriz de distancias originales, esta información está en el cuadro \(\ref{tab:comparacion_coef}\). Entre más cercano este el coeficiente de correlación a 1 nos indica que el dendrograma refleja mejor las distancias originales.
##
## Attaching package: 'kableExtra'## The following object is masked from 'package:dplyr':
##
## group_rows# vector con nombre de los métodos
m <- c( "average", "single", "complete", "ward.D2", "median", "centroid")
names(m) <- c( "average", "single", "complete", "ward.D2", "median", "centroid")
# Función para calcular el coeficiente de correlación
coef_cor <- function(x) {
cor(x=dist, cophenetic(hclust(d=dist, method = x)))
}
# Tabla comparativa
coef_tabla <- map_dbl(m, coef_cor)
kbl(coef_tabla, booktabs = TRUE, align = "c",
caption = "Cuadro comparativo de los coeficientes de correlación",
col.names = rownames(coef_tabla)) %>%
kable_styling(position = "center",
latex_options = c("repeat_header", "hold_position"),
font_size = 9) %>%
add_header_above(c("Método", "Coeficiente de correlación"))| average | 0.5589576 |
| single | 0.1104763 |
| complete | 0.5068456 |
| ward.D2 | 0.5096508 |
| median | 0.5548300 |
| centroid | 0.5490947 |
Podemos observar que el dendrograma que mejor refleja la similitud entre las observaciones es la del método average y el segundo mejor es el del método median. Vamos a usar el dendrograma de average ya que es en el que se visualizan mejor los grupos que se forman.
Para determinar cuantos grupos nos conviene más tomar, usamos dos métodos: el método del codo y el paquete NbClust. Este paquete usa 30 índices para determinar el número más relevante de clústers variando todas las combinaciones de número de clústers, distancias y métodos.
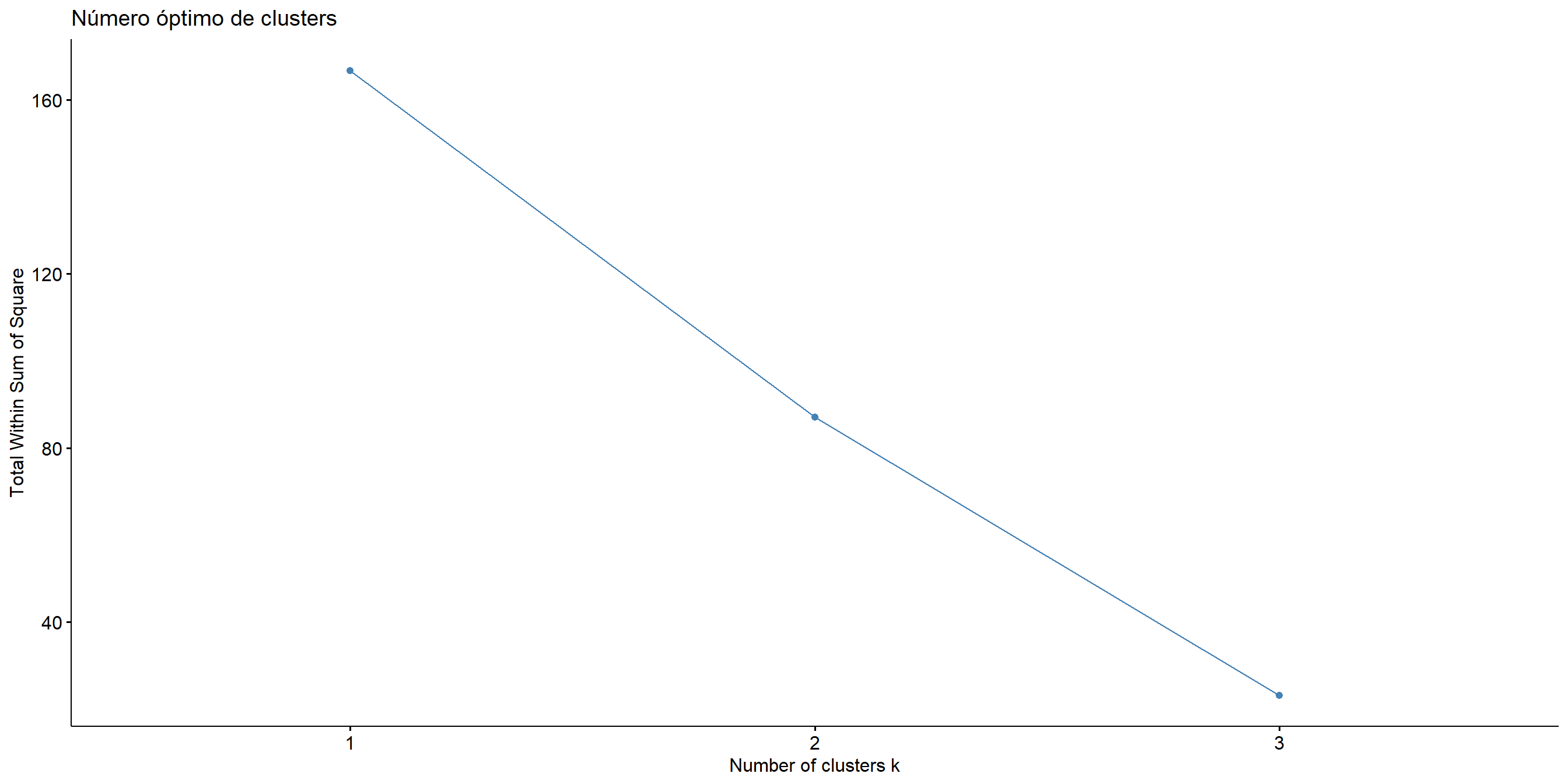
Figure 8.13: Número óbtimo de clusters usando el método del codo
Podemos observar en la gráfica de codo que en 3 es donde se forma el codo, así que esto nos diría que debemos considerar 3 clústers.
Usando el paquete ‘NbClust’ se pueden obtener una comparación del número óptimo de clústers.
Ejercicio: Carga la base de datos USArrests. Obtén los dendrogramas y compara cuales realizan una mejor agrupación. ¿Cuál es el número óptimo de clusters?
#Código de la clase
library(tidyverse)
library(cluster)
library(factoextra)
library(ggplot2)
library(purrr)
library(NbClust)
# Cargar datos y analizar varianzas y correlaciones
data("USArrests")
any(is.na(USArrests))
summary(USArrests)
dim(USArrests)
var(data.matrix(USArrests))
cor.mat_all <- cor(data.matrix(USArrests), use="complete.obs")
cor.mat_all
# Escalar datos
US_df <- scale(USArrests)
var(US_df)
# Calcular distancias
dist <- dist(US_df, method = "euclidean")
head(dist)
# Realizar clusters
cluster_single <- hclust (d = dist, method = 'single')
plot(cluster_single,cex=0.7, hang = -2)
cluster_complete <- hclust (d = dist, method = 'complete')
plot(cluster_complete, cex=0.7, hang = -2)
cluster_average <- hclust (d = dist, method = 'average')
plot(cluster_average, cex=0.7, hang = -2)
cluster_ward <- hclust (d = dist, method = 'ward.D2')
plot(cluster_ward,cex=0.7, hang = -2)
par (mfrow = c(2,2))
plot(cluster_single,cex=0.7, hang = -2)
plot(cluster_complete,cex=0.7, hang = -2)
plot(cluster_average,cex=0.7, hang = -2)
plot(cluster_ward,cex=0.7, hang = -2)
par (mfrow = c(1,1))
# Comparar coeficiente de correlación de los métodos
# vector con nombre de los métodos
m <- c( "average", "single", "complete", "ward.D2", "median", "centroid")
names(m) <- c( "average", "single", "complete", "ward.D2", "median", "centroid")
# Función para calcular el coeficiente de correlación
coef_cor <- function(x) {
cor(x=dist, cophenetic(hclust(d=dist, method = x)))
}
# Tabla comparativa
coef_tabla <- map_dbl(m, coef_cor)
coef_tabla
# Calcular número óptimo de clusters
# Método del codo
fviz_nbclust(x = US_df, FUNcluster = hcut, method = "wss", diss = dist, k.max = 7) +
labs(title = "Número óptimo de clusters") +
xlab("Número de clústers")
# Aplicar todos los índices y métodos
res.nbclust <- NbClust(US_df, distance = "euclidean",
min.nc = 3, max.nc = 6,
method = "average", index ="all")
# Realizar plot con el número óptimo de cluster y marcar los grupos
plot(cluster_average, cex = 0.6, hang = -2)
rect.hclust(cluster_average, k = 4, border = 2:8)
#fviz_nbclust(res.nbclust) +
# theme_minimal() +
# ggtitle("Número óbtimo de clusters con NbClust")
# Con Factoextra
# Matriz de distancias
fviz_dist(dist.obj = dist, lab_size = 8)
# Clusters
set.seed(12345)
hc_single <- hclust(d=dist, method = "single")
hc_average <- hclust(d=dist, method = "average")
hc_complete <- hclust(d=dist, method = "complete")
hc_ward <- hclust(d=dist, method = "ward.D2")
hc_median <- hclust(d=dist, method = "median")
hc_centroid <- hclust(d=dist, method = "centroid")
fviz_dend(x = hc_complete, k=4,
cex = 0.7,
main = "Cluster método complete",
xlab = "Ciudades",
ylab = "Distancias",
type= "rectangle",
sub = "",
horiz = TRUE)+
geom_hline(yintercept = 3.8, linetype = "dashed")
sub_grp <- cutree(hc_complete, k = 4)
table(sub_grp)
fviz_cluster(list(data = US_df, cluster = sub_grp))
# Comparar dendrogramas
library(dendextend)
hc_single <- agnes(US_df, method = "single")
hc_complete <- agnes(US_df, method = "complete")
hc_single <- as.dendrogram(hc_single)
hc_complete <- as.dendrogram(hc_complete)
tanglegram(rank_branches(hc_single),rank_branches(hc_complete),
main_left = "Single",
main_right = "Complete", lab.cex= 0.7, margin_inner = 5, k_branches = 4)8.4 Análisis de Componentes Principales
El análisis de componenetes principales tiene como objetivo reducir la dimensión y conservar en lo posible su estructura, es decir la forma de la nube de datos para esto el primer paro es obtener la matriz de correlaciones y la matriz de covarianzas.
Cuando se trabaja con distintas unidades de medición, conviene hacer el análisis de componentes principales haciendo los cálculos con la matriz R de correlaciones.
En R existen varios paquetes que nos permiten realizar análisis de componentes principales. Algunas de las funciones son prcomp(), princomp(), PCA().
Los argumentos de la función prcomp() son:
x: una matriz numérica o dataframe.scale: un valor lógico indicando si las variables deberían ser escaladas para tener varianza unitaria antes de realizar el análisis.
Los argumentos de princomp() son los siguientes:
x: una matrix numérica o dataframe.cor: un valor lógico indicando si los datos se centraran y escalaran antes de realizar el análisis.scores: un valor lógico indicando si se calcularan las coordenadas de cada componente principal.
Ambas funciones nos regresan los siguientes valores:
sdev: las desviaciones estándar de las componentes principales.rotation,loadings: la matriz de las cargas donde las columnas son los eigenvectores.center: las medias de las variables, las que fueron restadas.scale: las desviaciones estandar de las variables.x,scores: las coordenadas de las observaciones/individuos de las componentes principales.
Vamos a usar el paquete factoextra para visualizar los resultados.
Vamos a cargar la base de datos siguiente:
## New names:
## • `` -> `...1`## # A tibble: 6 × 8
## ...1 `100m` `200m` `400m` `800m` `1500m` `3000m` Marathon
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 argentin 11.6 22.9 54.5 2.15 4.43 9.79 179.
## 2 australi 11.2 22.4 51.1 1.98 4.13 9.08 152.
## 3 austria 11.4 23.1 50.6 1.99 4.22 9.34 159.
## 4 belgium 11.4 23.0 52 2 4.14 8.88 158.
## 5 bermuda 11.5 23.0 53.3 2.16 4.58 9.81 170.
## 6 brazil 11.3 23.2 52.8 2.1 4.49 9.77 169.¿Necesitamos escalar los datos? ¿Cómo son las varianzas y covarianzas? ¿Es conveniente trabajar con la matriz de correlación en vez de con la de varianzas y covarianzas?
¿Es apropiado hacer un análisis de componentes principales? ¿por qué? Si lo es, ya que hay muchas correlaciones altas, entonces se podría disminuir la dimensión.
library(corrplot)
res1 <- cor.mtest(records2, conf.level= .95)
res2 <- cor.mtest(records2, conf.level= .99)
cor.mat <- cor(records2, use="complete.obs")
corrplot(cor.mat)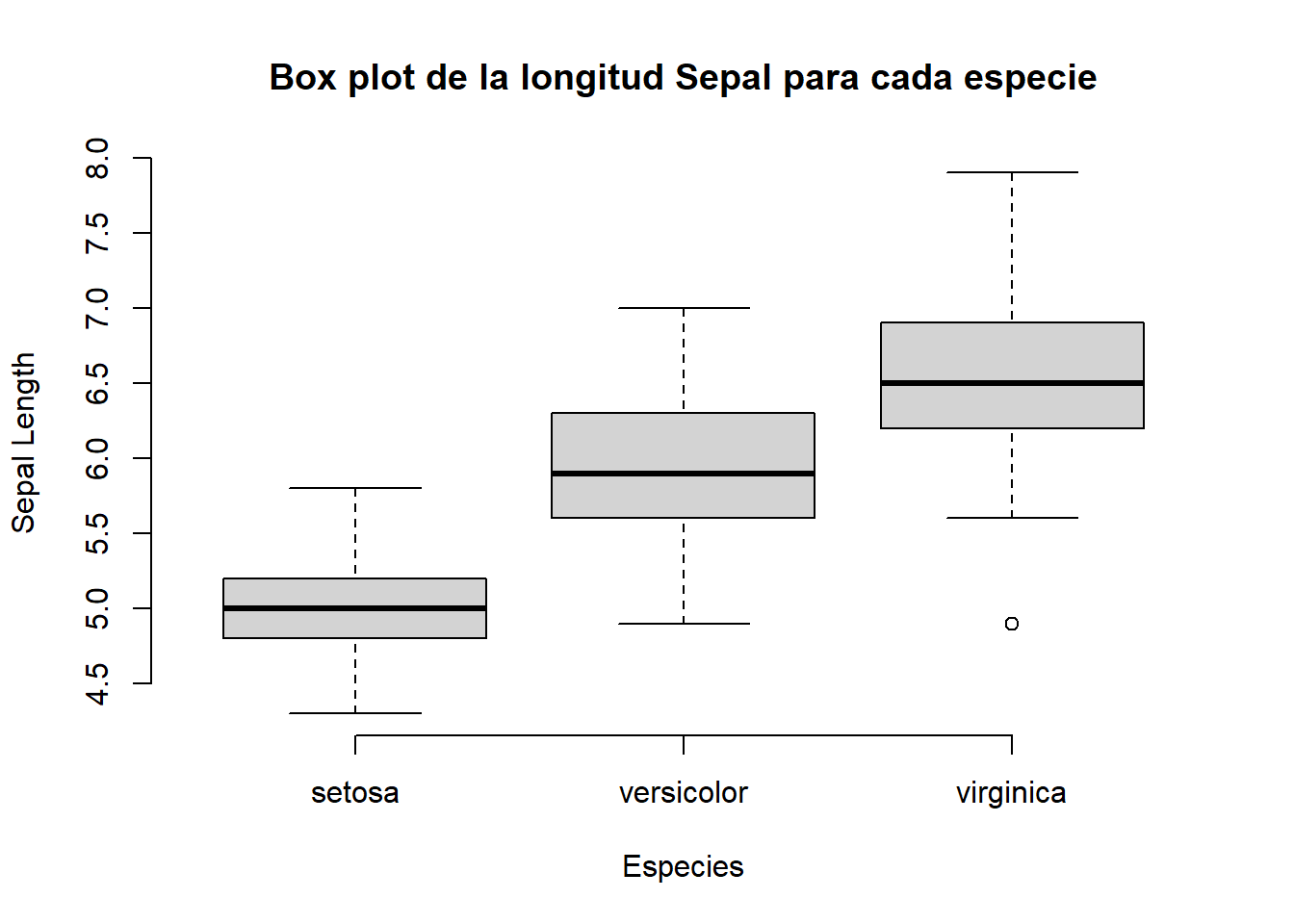
Para verificar que la matriz sea factorizable, la prueba que podemos aplicar es el criterio de Kaiser-Meyer-Olkin. La prueba de Kaiser-Meyer-Olkin (KMO) es una medida de qué tan adecuados son sus datos para el análisis factorial . La prueba mide la adecuación del muestreo para cada variable en el modelo y para el modelo completo. La estadística es una medida de la proporción de varianza entre variables que podrían ser varianza común. Como referencia, Kaiser puso los siguientes valores en los resultados:
| Rango | Clasificación |
|---|---|
| 0.00 a 0.49 | inaceptable. |
| 0.50 a 0.59 | miserable. |
| 0,60 a 0,69 | mediocre. |
| 0.70 a 0.79 | medio. |
| 0,80 a 0,89 | meritorio. |
| 0.90 a 1.00 | maravilloso. |
##
## Attaching package: 'psych'## The following objects are masked from 'package:ggplot2':
##
## %+%, alpha## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = records2)
## Overall MSA = 0.84
## MSA for each item =
## 100m 200m 400m 800m 1500m 3000m Marathon
## 0.83 0.80 0.84 0.83 0.82 0.84 0.93Vamos a calcular los componentes principales primero con la función princomp.
## Importance of components:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
## Standard deviation 2.4094991 0.80848347 0.54761522 0.35422802 0.231984732
## Proportion of Variance 0.8293837 0.09337793 0.04284035 0.01792536 0.007688131
## Cumulative Proportion 0.8293837 0.92276161 0.96560196 0.98352731 0.991215445
## Comp.6 Comp.7
## Standard deviation 0.197608919 0.149808546
## Proportion of Variance 0.005578469 0.003206086
## Cumulative Proportion 0.996793914 1.000000000Con la instrucción loadings lo que obtenemos son las cargas de los componentes principales. Es decir, lo que obtenemos son los coeficientes que se usarán en las combinaciones lineales para calcular cada componente principal. Por ejemplo, para un conjunto de datos \(X_1, X_2,..., X_p\) la primera columna que está denotada por Comp.1 tiene los coeficientes \(\phi_{11}, \phi_{21},... ,\phi_{p1}\) de la combinación lineal con la que se obtiene la primera componente principal:
\[Z_1=\phi_{11}X_1+\phi_{21}X_2+... +\phi_{p1}X_p\]
Esta primera componente principal será la que refleje la mayor variabilidad de los datos. Las cargas son las entradas de cada eigenvector son las siguientes:
##
## Loadings:
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## 100m 0.368 0.490 0.286 0.319 0.231 0.620
## 200m 0.365 0.537 0.230 -0.711 -0.109
## 400m 0.382 0.247 -0.515 -0.347 -0.572 0.191 0.208
## 800m 0.385 -0.155 -0.585 0.620 -0.315
## 1500m 0.389 -0.360 0.430 -0.231 0.693
## 3000m 0.389 -0.348 0.153 0.363 -0.463 -0.598
## Marathon 0.367 -0.369 0.484 -0.672 0.131 0.142
##
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## SS loadings 1.000 1.000 1.000 1.000 1.000 1.000 1.000
## Proportion Var 0.143 0.143 0.143 0.143 0.143 0.143 0.143
## Cumulative Var 0.143 0.286 0.429 0.571 0.714 0.857 1.000Usando estos valores, la fórmula de la primer componente principal se escribiría como:
\[(0.368, 0.365, 0.382,0.385,0.389, 0.389.0.367)(100m-mean(100m), 200m-mean(200m),...,Marathon-mean(Marathon))\]
Las desviaciones estándar son las raíces de las lambdas.
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## 2.4094991 0.8084835 0.5476152 0.3542280 0.2319847 0.1976089 0.1498085Para calcular la varianza debemos elevar al cuadrado cada una de las entradas.
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## 5.80568576 0.65364552 0.29988243 0.12547749 0.05381692 0.03904928 0.02244260Para obtener la proporción de la varianza que explica cada componente lo que tenemos que hacer es dividir el valor de la varianza de la componente \(j\) entre la suma de las varianzas de todas las componentes.
El siguiente código muestra como realizarlo. Además, en la instrucción summary vemos que estos valores coinciden con los de la segunda fila.
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6
## 0.829383680 0.093377931 0.042840347 0.017925356 0.007688131 0.005578469
## Comp.7
## 0.003206086Si lo que queremos es el porcentaje, entonces solo hay que multiplicar por 100
Para encontrar la proporción de varianza acumulada, lo que tenemos que hacer es dividir la suma de los primeros \(j-\)ésimos eigenvalores entre entre la suma de todos los eigenvalores.
Cálculamos los eigenvalores de la matriz cuadrada de correlación.
La varianza de las Componentes Principales, es igual a los eigenvalores. Es decir, la desviación estándar de las componentes, es igual a la raíz de los valores propios.
## Comp.1 Comp.2 Comp.3 Comp.4 Comp.5 Comp.6 Comp.7
## TRUE TRUE TRUE TRUE TRUE TRUE TRUEPor otra parte, se puede afirmar que la traza de la matriz lambda es igual a la suma de la varianza de cada valor observado.
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 5.81 0.00 0.0 0.00 0.00 0.00 0.00
## [2,] 0.00 0.65 0.0 0.00 0.00 0.00 0.00
## [3,] 0.00 0.00 0.3 0.00 0.00 0.00 0.00
## [4,] 0.00 0.00 0.0 0.13 0.00 0.00 0.00
## [5,] 0.00 0.00 0.0 0.00 0.05 0.00 0.00
## [6,] 0.00 0.00 0.0 0.00 0.00 0.04 0.00
## [7,] 0.00 0.00 0.0 0.00 0.00 0.00 0.02## [1] 7Además, el porcentaje de la varianza generalizada que es explicado por la componente \(j\)-ésima es igual a la relación que hay entre los eigenvalores divididos por la suma de la diagonal de eigenvalores. Es decir, esto es igual al porcentaje de varianza acumulada por la función summary, y hecho a mano con la suma acumulada de los valores propios.
## [1] 0.8293837 0.9227616 0.9656020 0.9835273 0.9912154 0.9967939 1.0000000Esta matriz es la diagonal con los eigenvalores.
## [,1] [,2] [,3] [,4] [,5] [,6] [,7]
## [1,] 5.81 0.00 0.0 0.00 0.00 0.00 0.00
## [2,] 0.00 0.65 0.0 0.00 0.00 0.00 0.00
## [3,] 0.00 0.00 0.3 0.00 0.00 0.00 0.00
## [4,] 0.00 0.00 0.0 0.13 0.00 0.00 0.00
## [5,] 0.00 0.00 0.0 0.00 0.05 0.00 0.00
## [6,] 0.00 0.00 0.0 0.00 0.00 0.04 0.00
## [7,] 0.00 0.00 0.0 0.00 0.00 0.00 0.02La traza de la matriz \(\Lambda\) es igual a la suma de las varianzas acumuladas por los Componentes.
## [1] 7Una forma de ver con cuantos componentes nos conviene trabajar es con el gráfico de codo.
¿Con cuántas componentes nos conviene quedarnos?
El biplot es una forma de representar los resultados de PCA.
Vamos a analizar el biplot a detalle.
¿Qué mide la primera componente? o ¿Cómo la interpretas?
La interpretación no se hace en función delos individuos sino de las variables que explica cada componente. Como en esta primer componente, todas las cargas son positivas y muy similares para todas las variables, podríamos nombrar a esta variable “velocidad en las carreras” por ejemplo.
En el biplot, los países que quedan a la derecha del cero, ¿qué tipo de corredores tienen? Los lentos.
En el biplot, los países que quedan con puntajes altos en la segunda componente, tienen velocistas rápidos y fondistas lentos o viceversa?
Los pesos positivos están en las carreras de velocidad y los pesos negativos en las de fondo. Es decir, un país con valores altos (tiempos grandes) en las carreras X100, X200, X400, tendrá valores positivos y grandes al multiplicar por las cargas de componente 2, y sí tiene tiempos bajos en las carreras de fondo, al multiplicar por las cargas negativas de la componente 2, el score para ese país en el componente 2 será positivo. Caso contrario pasaría con un país con tiempos cortos en las carreras de 100 a 200 m, y tiempos largos en las carreras de fondo.
¿En qué cuadrante se encuentran los países que tienen a los velocistas más rápidos? Sería III, pues es el cuadrante opuesto a la dirección de los vectores de las variables X100, X200, X400 ( cuadrante I, en donde se ubican los velocistas más lentos).
¿En qué cuadrante se encuentran los países que tienen a los fondistas más rápidos? Sería el cuadrante II, opuesto a la dirección de los vectores de marathon, X800, X1500 (ubicados en cuadrante IV, en donde están los fondistas mas lentos).
¿Qué país tiene los velocistas más lentos? Sí observas el biplot CP1 vs CP2, Cookis está hacia donde están apuntando los vectores positivos de las carreras de velocidad, lo cual quiere decir que ese país tiene tiempos largos en esas carreras de velocidad y en consecuencia, su score en componente 2 resulta muy positiva.
¿Qué país tiene los fondistas más lentos?
Sí observas el biplot CP1 vs CP2, wsamoa está hacia donde están apuntando los vectores de las carreras de fondo (X800, X1500, Xmarathon), lo cual quiere decir que ese país tiene tiempos largos en esas carreras de fondo y en consecuencia, su score en componente 2 resulta muy negativa.
8.4.1 Ejemplo 2
Vamos a cargar la base de datos decathlon2 del paquete factoextra y vamos a extraer los individuos del 1:23 y las variables 1:10.
## X100m Long.jump Shot.put High.jump X400m X110m.hurdle
## SEBRLE 11.04 7.58 14.83 2.07 49.81 14.69
## CLAY 10.76 7.40 14.26 1.86 49.37 14.05
## BERNARD 11.02 7.23 14.25 1.92 48.93 14.99
## YURKOV 11.34 7.09 15.19 2.10 50.42 15.31
## ZSIVOCZKY 11.13 7.30 13.48 2.01 48.62 14.17
## McMULLEN 10.83 7.31 13.76 2.13 49.91 14.38¿Necesitamos escalar los datos? ¿Cómo son las varianzas y covarianzas?
Vamos a calcular la matriz de correlaciones y verificar que sea factorizable.
library(corrplot)
res1 <- cor.mtest(decathlon2_activos, conf.level= .95)
res2 <- cor.mtest(decathlon2_activos, conf.level= .99)
cor.mat <- cor(decathlon2_activos, use="complete.obs")
corrplot(cor.mat)
## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = decathlon2_activos)
## Overall MSA = 0.68
## MSA for each item =
## X100m Long.jump Shot.put High.jump X400m X110m.hurdle
## 0.77 0.88 0.60 0.59 0.78 0.81
## Discus Pole.vault Javeline X1500m
## 0.64 0.38 0.76 0.40Removemos algunas de las variables para ver si el valor del test sube.
library(tidyverse)
base.cp1 <- decathlon2_activos
base.cp1 <- base.cp1 %>%
dplyr::select(-Pole.vault)
kmo.2 <- KMO(base.cp1)
kmo.2## Kaiser-Meyer-Olkin factor adequacy
## Call: KMO(r = base.cp1)
## Overall MSA = 0.74
## MSA for each item =
## X100m Long.jump Shot.put High.jump X400m X110m.hurdle
## 0.75 0.88 0.72 0.73 0.76 0.79
## Discus Javeline X1500m
## 0.77 0.68 0.30
Usaremos la función prcomp() y primero realizaremos el análisis sin quitar la variable anterior.
Visualizamos lo eigenvalores.
## Importance of components:
## PC1 PC2 PC3 PC4 PC5 PC6 PC7
## Standard deviation 2.0308 1.3559 1.1132 0.90523 0.83759 0.65029 0.55007
## Proportion of Variance 0.4124 0.1839 0.1239 0.08194 0.07016 0.04229 0.03026
## Cumulative Proportion 0.4124 0.5963 0.7202 0.80213 0.87229 0.91458 0.94483
## PC8 PC9 PC10
## Standard deviation 0.52390 0.39398 0.3492
## Proportion of Variance 0.02745 0.01552 0.0122
## Cumulative Proportion 0.97228 0.98780 1.0000¿Cuál es la proporción de la varianza explicada de las componentes?
¿Con cuántas componentes nos conviene quedarnos? ¿Porqué?
Vamos a graficar a los individuos y corolearlos por perfiles similares.
fviz_pca_ind(res.pca,
col.ind = "cos2", # color por la calidad de representación
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE # evitar que se sobrelape el texto
)
Para graficar las variables y ver sus correlaciones realizamos lo siguiente. Variables correlacionadas negativamente apuntan a lados opuestos.
fviz_pca_var(res.pca,
col.var = "contrib", # Color por contribución al PCA
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = TRUE
)
Un objeto importante en estos análisis de PCA son los biplots.
fviz_pca_biplot(res.pca, repel = TRUE,
col.var = "#2E9FDF", # Variables
col.ind = "#696969" # Individuos
)
fviz_pca_biplot(res.pca, repel = TRUE, axes = c(1,3),
col.var = "#2E9FDF", # Variables
col.ind = "#696969" # Individuos
)
Vamos a acceder a los resultados del PCA.
## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 4.1242133 41.242133 41.24213
## Dim.2 1.8385309 18.385309 59.62744
## Dim.3 1.2391403 12.391403 72.01885
## Dim.4 0.8194402 8.194402 80.21325
## Dim.5 0.7015528 7.015528 87.22878
## Dim.6 0.4228828 4.228828 91.45760
## Dim.7 0.3025817 3.025817 94.48342
## Dim.8 0.2744700 2.744700 97.22812
## Dim.9 0.1552169 1.552169 98.78029
## Dim.10 0.1219710 1.219710 100.00000## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## X100m -0.850625692 0.17939806 -0.30155643 0.03357320 -0.1944440
## Long.jump 0.794180641 -0.28085695 0.19054653 -0.11538956 0.2331567
## Shot.put 0.733912733 -0.08540412 -0.51759781 0.12846837 -0.2488129
## High.jump 0.610083985 0.46521415 -0.33008517 0.14455012 0.4027002
## X400m -0.701603377 -0.29017826 -0.28353292 0.43082552 0.1039085
## X110m.hurdle -0.764125197 0.02474081 -0.44888733 -0.01689589 0.2242200
## Discus 0.743209016 -0.04966086 -0.17652518 0.39500915 -0.4082391
## Pole.vault -0.217268042 -0.80745110 -0.09405773 -0.33898477 -0.2216853
## Javeline 0.428226639 -0.38610928 -0.60412432 -0.33173454 0.1978128
## X1500m 0.004278487 -0.78448019 0.21947068 0.44800961 0.2632527
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## X100m 0.035374780 -0.091336386 -0.104716925 -0.30306448 0.044417974
## Long.jump -0.033727883 -0.154330810 -0.397380703 -0.05158951 0.029719453
## Shot.put -0.239789034 -0.009886612 0.024359049 0.04778655 0.217451948
## High.jump -0.284644846 0.028157465 0.084405578 -0.11213822 -0.133566774
## X400m -0.049289996 0.286106008 -0.233552216 0.08216041 -0.034170673
## X110m.hurdle 0.002632395 -0.370072158 -0.008344682 0.16176025 -0.015629914
## Discus 0.198544870 -0.142725641 -0.039559255 0.01336209 -0.172590426
## Pole.vault -0.327464549 -0.010393176 0.032914942 -0.02576874 -0.137211339
## Javeline 0.362097598 0.133564318 0.052841099 -0.04045397 -0.003854347
## X1500m 0.042050151 -0.111367083 0.194469730 -0.10224014 0.062834809## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## X100m 1.754429e+01 1.7505098 7.3386590 0.13755240 5.389252
## Long.jump 1.529317e+01 4.2904162 2.9300944 1.62485936 7.748815
## Shot.put 1.306014e+01 0.3967224 21.6204325 2.01407269 8.824401
## High.jump 9.024811e+00 11.7715838 8.7928883 2.54987951 23.115504
## X400m 1.193554e+01 4.5799296 6.4876363 22.65090599 1.539012
## X110m.hurdle 1.415754e+01 0.0332933 16.2612611 0.03483735 7.166193
## Discus 1.339309e+01 0.1341398 2.5147385 19.04132022 23.755756
## Pole.vault 1.144592e+00 35.4618611 0.7139512 14.02307063 7.005084
## Javeline 4.446377e+00 8.1086683 29.4531777 13.42963254 5.577615
## X1500m 4.438531e-04 33.4728757 3.8871610 24.49386930 9.878367
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## X100m 0.295915322 2.75705260 3.99520353 59.1740009 1.61756139
## Long.jump 0.269003613 7.87159392 57.53322220 1.7146826 0.72414393
## Shot.put 13.596858744 0.03230371 0.21618512 1.4712015 38.76768578
## High.jump 19.159607001 0.26202607 2.59565787 8.1015517 14.62649091
## X400m 0.574509906 27.05274658 19.87344405 4.3489667 0.95730504
## X110m.hurdle 0.001638634 45.26163460 0.02537025 16.8579392 0.20028870
## Discus 9.321746508 6.73226823 0.57016606 0.1150295 24.42174410
## Pole.vault 25.357622290 0.03569883 0.39472201 0.4278065 15.43559151
## Javeline 31.004964393 5.89573984 1.01729950 1.0543458 0.01217993
## X1500m 0.418133591 4.09893563 13.77872941 6.7344755 3.23700871## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## X100m 7.235641e-01 0.0321836641 0.090936280 0.0011271597 0.03780845
## Long.jump 6.307229e-01 0.0788806285 0.036307981 0.0133147506 0.05436203
## Shot.put 5.386279e-01 0.0072938636 0.267907488 0.0165041211 0.06190783
## High.jump 3.722025e-01 0.2164242070 0.108956221 0.0208947375 0.16216747
## X400m 4.922473e-01 0.0842034209 0.080390914 0.1856106269 0.01079698
## X110m.hurdle 5.838873e-01 0.0006121077 0.201499837 0.0002854712 0.05027463
## Discus 5.523596e-01 0.0024662013 0.031161138 0.1560322304 0.16665918
## Pole.vault 4.720540e-02 0.6519772763 0.008846856 0.1149106765 0.04914437
## Javeline 1.833781e-01 0.1490803723 0.364966189 0.1100478063 0.03912992
## X1500m 1.830545e-05 0.6154091638 0.048167378 0.2007126089 0.06930197
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## X100m 1.251375e-03 0.0083423353 1.096563e-02 0.0918480768 1.972956e-03
## Long.jump 1.137570e-03 0.0238179990 1.579114e-01 0.0026614779 8.832459e-04
## Shot.put 5.749878e-02 0.0000977451 5.933633e-04 0.0022835540 4.728535e-02
## High.jump 8.102269e-02 0.0007928428 7.124302e-03 0.0125749811 1.784008e-02
## X400m 2.429504e-03 0.0818566479 5.454664e-02 0.0067503333 1.167635e-03
## X110m.hurdle 6.929502e-06 0.1369534023 6.963371e-05 0.0261663784 2.442942e-04
## Discus 3.942007e-02 0.0203706085 1.564935e-03 0.0001785453 2.978746e-02
## Pole.vault 1.072330e-01 0.0001080181 1.083393e-03 0.0006640282 1.882695e-02
## Javeline 1.311147e-01 0.0178394271 2.792182e-03 0.0016365234 1.485599e-05
## X1500m 1.768215e-03 0.0124026272 3.781848e-02 0.0104530472 3.948213e-03## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## SEBRLE 0.1912074 -1.5541282 -0.62836882 0.08205241 1.1426139415
## CLAY 0.7901217 -2.4204156 1.35688701 1.26984296 -0.8068483724
## BERNARD -1.3292592 -1.6118687 -0.19614996 -1.92092203 0.0823428202
## YURKOV -0.8694134 0.4328779 -2.47398223 0.69723814 0.3988584116
## ZSIVOCZKY -0.1057450 2.0233632 1.30493117 -0.09929630 -0.1970241089
## McMULLEN 0.1185550 0.9916237 0.84355824 1.31215266 1.5858708644
## MARTINEAU -2.3923532 1.2849234 -0.89816842 0.37309771 -2.2433515889
## HERNU -1.8910497 -1.1784614 -0.15641037 0.89130068 -0.1267412520
## BARRAS -1.7744575 0.4125321 0.65817750 0.22872866 -0.2338366980
## NOOL -2.7770058 1.5726757 0.60724821 -1.55548081 1.4241839810
## BOURGUIGNON -4.4137335 -1.2635770 -0.01003734 0.66675478 0.4191518468
## Sebrle 3.4514485 -1.2169193 -1.67816711 -0.80870696 -0.0250530746
## Clay 3.3162243 -1.6232908 -0.61840443 -0.31679906 0.5691645854
## Karpov 4.0703560 0.7983510 1.01501662 0.31336354 -0.7974259553
## Macey 1.8484623 2.0638828 -0.97928455 0.58469073 -0.0002157834
## Warners 1.3873514 -0.2819083 1.99969621 -1.01959817 -0.0405401497
## Zsivoczky 0.4715533 0.9267436 -1.72815525 -0.18483138 0.4073029909
## Hernu 0.2763118 1.1657260 0.17056375 -0.84869401 -0.6894795441
## Bernard 1.3672590 1.4780354 0.83137913 0.74531557 0.8598016482
## Schwarzl -0.7102777 -0.6584251 1.04075176 -0.92717510 -0.2887568007
## Pogorelov -0.2143524 -0.8610557 0.29761010 1.35560294 -0.0150531057
## Schoenbeck -0.4953166 -1.3000530 0.10300360 -0.24927712 -0.6452257128
## Barras -0.3158867 0.8193681 -0.86169481 -0.58935985 -0.7797389436
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## SEBRLE -0.46389755 -0.20796012 0.043460568 -0.659344137 0.03273238
## CLAY 1.30420016 -0.21291866 0.617240611 -0.060125359 -0.31716015
## BERNARD -0.40062867 -0.40643754 0.703856040 0.170083313 -0.09908142
## YURKOV 0.10286344 -0.32487448 0.114996135 -0.109524039 -0.11969720
## ZSIVOCZKY 0.89554111 0.08825624 -0.202341299 -0.523103099 -0.34842265
## McMULLEN 0.18657283 0.47828432 0.293089967 -0.105623196 -0.39317797
## MARTINEAU -0.45666350 -0.29975522 -0.291628488 -0.223417655 -0.61640509
## HERNU 0.43623496 -0.56609980 -1.529404317 0.006184409 0.55368016
## BARRAS 0.09026010 0.21594095 0.682583078 -0.669282042 0.53085420
## NOOL 0.49716399 -0.53205687 -0.433385655 -0.115777808 -0.09622142
## BOURGUIGNON -0.08200220 -0.59833739 0.563619921 0.525814030 0.05855882
## Sebrle -0.08279306 0.01016177 -0.030585843 -0.847210682 0.21970353
## Clay 0.77715960 0.25750851 -0.580638301 0.409776590 -0.61601933
## Karpov -0.32958134 -1.36365568 0.345306381 0.193055107 0.21721852
## Macey -0.19728082 -0.26927772 -0.363219506 0.368260269 0.21249474
## Warners -0.55673300 -0.26739400 -0.109470797 0.180283071 0.24208420
## Zsivoczky -0.11383190 0.03991159 0.538039776 0.585966156 -0.14271715
## Hernu -0.33168404 0.44308686 0.247293566 0.066908586 -0.20868256
## Bernard -0.32806564 0.36357920 0.006165316 0.279488675 0.32067773
## Schwarzl -0.68891640 0.56568604 -0.687053339 -0.008358849 -0.30211546
## Pogorelov -1.59379599 0.78370119 -0.037623661 -0.130531397 -0.03697576
## Schoenbeck 0.16172381 0.85752368 -0.255850722 0.564222295 0.29680481
## Barras 1.17415412 0.94512710 0.365550568 0.102255763 0.61186706## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## SEBRLE 0.03854254 5.7118249 1.385418e+00 0.03572215 8.091161e+00
## CLAY 0.65814114 13.8541889 6.460097e+00 8.55568792 4.034555e+00
## BERNARD 1.86273218 6.1441319 1.349983e-01 19.57827284 4.202070e-02
## YURKOV 0.79686310 0.4431309 2.147558e+01 2.57939100 9.859373e-01
## ZSIVOCZKY 0.01178829 9.6816398 5.974848e+00 0.05231437 2.405750e-01
## McMULLEN 0.01481737 2.3253860 2.496789e+00 9.13531719 1.558646e+01
## MARTINEAU 6.03367104 3.9044125 2.830527e+00 0.73858431 3.118936e+01
## HERNU 3.76996156 3.2842176 8.583863e-02 4.21505626 9.955149e-02
## BARRAS 3.31942012 0.4024544 1.519980e+00 0.27758505 3.388731e-01
## NOOL 8.12988880 5.8489726 1.293851e+00 12.83761115 1.257025e+01
## BOURGUIGNON 20.53729577 3.7757623 3.534995e-04 2.35877858 1.088816e+00
## Sebrle 12.55838616 3.5020697 9.881482e+00 3.47006223 3.889859e-03
## Clay 11.59361384 6.2315181 1.341828e+00 0.53250375 2.007648e+00
## Karpov 17.46609555 1.5072627 3.614914e+00 0.52101693 3.940874e+00
## Macey 3.60207087 10.0732890 3.364879e+00 1.81387486 2.885677e-07
## Warners 2.02910262 0.1879390 1.403071e+01 5.51585696 1.018550e-02
## Zsivoczky 0.23441891 2.0310492 1.047894e+01 0.18126182 1.028128e+00
## Hernu 0.08048777 3.2136178 1.020764e-01 3.82170515 2.946148e+00
## Bernard 1.97075488 5.1661961 2.425213e+00 2.94737426 4.581507e+00
## Schwarzl 0.53184785 1.0252129 3.800546e+00 4.56119277 5.167449e-01
## Pogorelov 0.04843819 1.7533304 3.107757e-01 9.75034337 1.404313e-03
## Schoenbeck 0.25864068 3.9969003 3.722687e-02 0.32970059 2.580092e+00
## Barras 0.10519467 1.5876667 2.605305e+00 1.84296038 3.767994e+00
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## SEBRLE 2.21256620 0.621426384 2.992045e-02 12.177477305 0.03819185
## CLAY 17.48801877 0.651413899 6.035125e+00 0.101262442 3.58568943
## BERNARD 1.65019840 2.373652810 7.847747e+00 0.810319793 0.34994507
## YURKOV 0.10878629 1.516564073 2.094806e-01 0.336009790 0.51072064
## ZSIVOCZKY 8.24561722 0.111923276 6.485544e-01 7.664919832 4.32741147
## McMULLEN 0.35788945 3.287016354 1.360753e+00 0.312501167 5.51053518
## MARTINEAU 2.14409841 1.291109482 1.347216e+00 1.398195851 13.54402896
## HERNU 1.95655942 4.604850849 3.705288e+01 0.001071345 10.92781554
## BARRAS 0.08376135 0.670038259 7.380544e+00 12.547331617 10.04537028
## NOOL 2.54127369 4.067669683 2.975270e+00 0.375477289 0.33003418
## BOURGUIGNON 0.06913582 5.144247534 5.032108e+00 7.744571086 0.12223626
## Sebrle 0.07047579 0.001483775 1.481898e-02 20.105546253 1.72063803
## Clay 6.20972751 0.952824148 5.340583e+00 4.703566841 13.52708188
## Karpov 1.11680500 26.720158115 1.888802e+00 1.043988269 1.68193477
## Macey 0.40014909 1.041910483 2.089853e+00 3.798767930 1.60957713
## Warners 3.18673563 1.027384225 1.898339e-01 0.910422384 2.08904756
## Zsivoczky 0.13322327 0.022889042 4.585705e+00 9.617852173 0.72605208
## Hernu 1.13110069 2.821027418 9.687304e-01 0.125399768 1.55234328
## Bernard 1.10655655 1.899449022 6.021268e-04 2.188071254 3.66566729
## Schwarzl 4.87961053 4.598122119 7.477531e+00 0.001957159 3.25357879
## Pogorelov 26.11665608 8.825322559 2.242329e-02 0.477268755 0.04873597
## Schoenbeck 0.26890572 10.566272800 1.036933e+00 8.917302863 3.14020004
## Barras 14.17432302 12.835417603 2.116763e+00 0.292892746 13.34533825## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## SEBRLE 0.007530179 0.49747323 8.132523e-02 0.001386688 2.689027e-01
## CLAY 0.048701249 0.45701660 1.436281e-01 0.125791741 5.078506e-02
## BERNARD 0.197199804 0.28996555 4.294015e-03 0.411819183 7.567259e-04
## YURKOV 0.096109800 0.02382571 7.782303e-01 0.061812637 2.022798e-02
## ZSIVOCZKY 0.001574385 0.57641944 2.397542e-01 0.001388216 5.465497e-03
## McMULLEN 0.002175437 0.15219499 1.101379e-01 0.266486530 3.892621e-01
## MARTINEAU 0.404013915 0.11654676 5.694575e-02 0.009826320 3.552552e-01
## HERNU 0.399282749 0.15506199 2.731529e-03 0.088699901 1.793538e-03
## BARRAS 0.616241975 0.03330700 8.478249e-02 0.010239088 1.070152e-02
## NOOL 0.489872515 0.15711146 2.342405e-02 0.153694675 1.288433e-01
## BOURGUIGNON 0.859698130 0.07045912 4.446015e-06 0.019618511 7.753120e-03
## Sebrle 0.675380606 0.08395940 1.596674e-01 0.037079012 3.558507e-05
## Clay 0.687592867 0.16475409 2.391051e-02 0.006274965 2.025440e-02
## Karpov 0.783666922 0.03014772 4.873187e-02 0.004644764 3.007790e-02
## Macey 0.363436037 0.45308203 1.020057e-01 0.036362957 4.952707e-09
## Warners 0.255651956 0.01055582 5.311341e-01 0.138081100 2.182965e-04
## Zsivoczky 0.045053176 0.17401353 6.051030e-01 0.006921739 3.361236e-02
## Hernu 0.024824321 0.44184663 9.459148e-03 0.234196727 1.545686e-01
## Bernard 0.289347476 0.33813318 1.069834e-01 0.085980212 1.144234e-01
## Schwarzl 0.116721435 0.10030142 2.506043e-01 0.198892209 1.929118e-02
## Pogorelov 0.007803472 0.12591966 1.504272e-02 0.312101619 3.848427e-05
## Schoenbeck 0.067070098 0.46204603 2.900467e-03 0.016987442 1.138116e-01
## Barras 0.018972684 0.12765099 1.411800e-01 0.066043061 1.156018e-01
## Dim.6 Dim.7 Dim.8 Dim.9 Dim.10
## SEBRLE 0.0443241299 8.907507e-03 3.890334e-04 8.954067e-02 0.0002206741
## CLAY 0.1326907339 3.536548e-03 2.972084e-02 2.820119e-04 0.0078471026
## BERNARD 0.0179131165 1.843634e-02 5.529104e-02 3.228572e-03 0.0010956493
## YURKOV 0.0013453555 1.341980e-02 1.681440e-03 1.525225e-03 0.0018217256
## ZSIVOCZKY 0.1129176906 1.096685e-03 5.764478e-03 3.852703e-02 0.0170924251
## McMULLEN 0.0053876990 3.540616e-02 1.329562e-02 1.726733e-03 0.0239268142
## MARTINEAU 0.0147210347 6.342774e-03 6.003515e-03 3.523552e-03 0.0268211980
## HERNU 0.0212478795 3.578167e-02 2.611676e-01 4.270425e-06 0.0342288717
## BARRAS 0.0015944528 9.126203e-03 9.118662e-02 8.766746e-02 0.0551531863
## NOOL 0.0157010551 1.798232e-02 1.193105e-02 8.514912e-04 0.0005881295
## BOURGUIGNON 0.0002967459 1.579887e-02 1.401866e-02 1.220108e-02 0.0001513277
## Sebrle 0.0003886276 5.854423e-06 5.303795e-05 4.069384e-02 0.0027366539
## Clay 0.0377627839 4.145976e-03 2.107924e-02 1.049876e-02 0.0237264222
## Karpov 0.0051379747 8.795817e-02 5.639959e-03 1.762907e-03 0.0022318265
## Macey 0.0041397727 7.712721e-03 1.403282e-02 1.442502e-02 0.0048028954
## Warners 0.0411689767 9.496848e-03 1.591742e-03 4.317040e-03 0.0077841113
## Zsivoczky 0.0026253777 3.227467e-04 5.865332e-02 6.956790e-02 0.0041268259
## Hernu 0.0357707217 6.383462e-02 1.988402e-02 1.455601e-03 0.0141595965
## Bernard 0.0166586433 2.046050e-02 5.883405e-06 1.209056e-02 0.0159167991
## Schwarzl 0.1098063093 7.403638e-02 1.092132e-01 1.616543e-05 0.0211173850
## Pogorelov 0.4314162233 1.043115e-01 2.404103e-04 2.893750e-03 0.0002322016
## Schoenbeck 0.0071500829 2.010275e-01 1.789520e-02 8.702893e-02 0.0240826922
## Barras 0.2621297474 1.698426e-01 2.540745e-02 1.988116e-03 0.0711836486El conjunto de datos tiene unas variables categóricas en la columna 13 que se quitó al inicio que corresponde al tipo de competición. Vamos a usar esa variable para agrupar los individuos.
groups <- as.factor(decathlon2$Competition[1:23])
fviz_pca_ind(res.pca,
col.ind = groups, # color by groups
palette = c("#00AFBB", "#FC4E07"),
addEllipses = TRUE, # Concentration ellipses
ellipse.level=0.7,
legend.title = "Groups",
repel = TRUE
)
Explica las componentes. ¿Cómo podrías llamar a las componentes 1 y 2?
Ejercicio: Carga la base de datos siguiente y realiza el análisis de componentes principales. Decide y justifica que matriz usaras, la de varianzas y covarianzas o la de correlaciones. ¿Con cuántas componentes te quedarías? ¿por qué? ¿Qué explica cada componente de las que te quedaste? ¿Cuál es la varianza total explicada por esas componentes? ¿Qué tortuga es la más grande? ¿Qué variable tiene la mayor varianza? ¿Las variables están correlacionadas positivamente? ¿Porqué?
library(readr)
turtledata <- read_delim("data/turtledata.csv",
delim = ";", escape_double = FALSE, trim_ws = TRUE)## Rows: 48 Columns: 4
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ";"
## dbl (4): length, width, height, female
##
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.## length width height
## length 420.0408 254.0452 165.09043
## width 254.0452 160.6769 101.78989
## height 165.0904 101.7899 69.98404## length width height
## length 1.0000000 0.9778869 0.9628899
## width 0.9778869 1.0000000 0.9599055
## height 0.9628899 0.9599055 1.0000000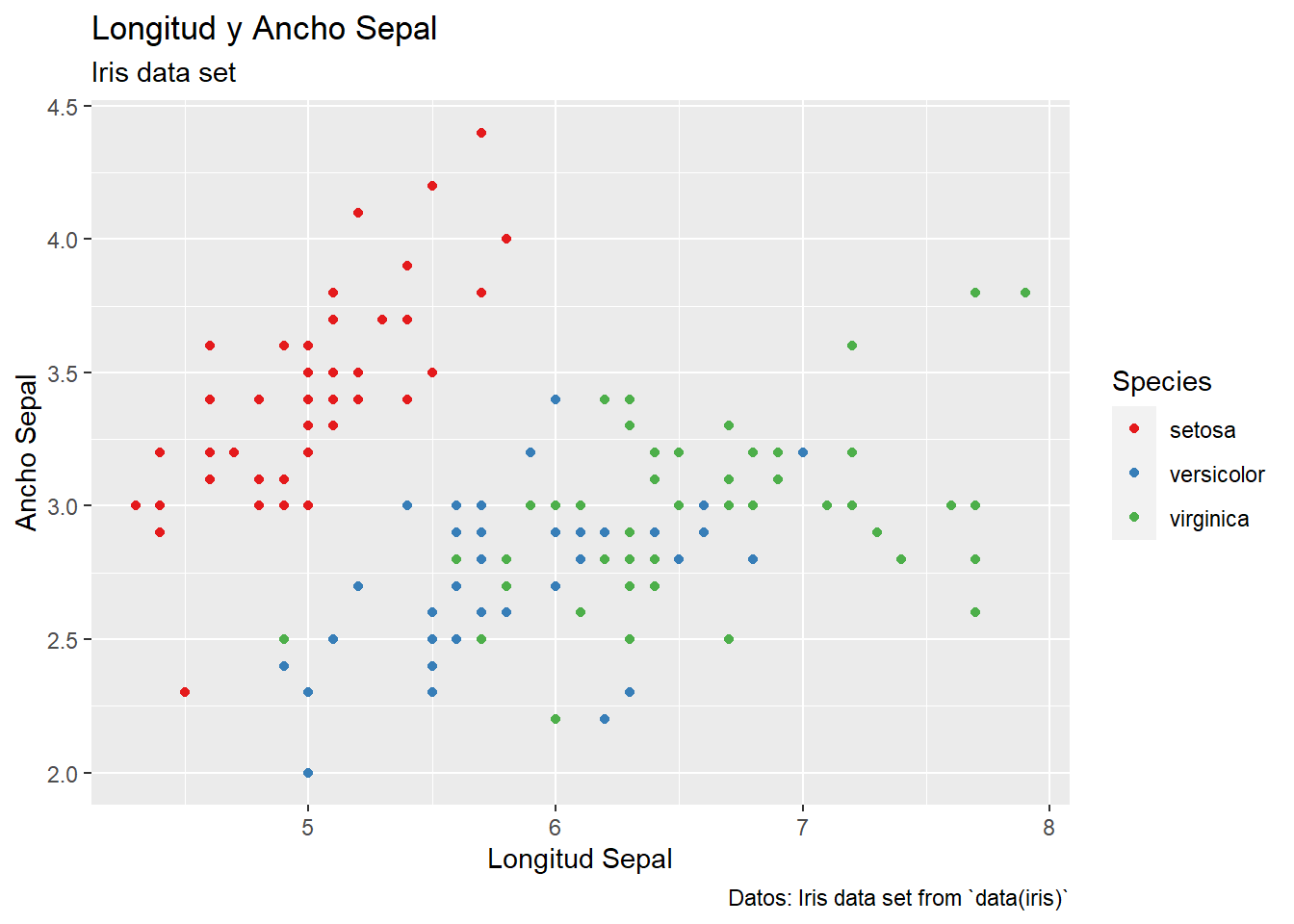
## Importance of components:
## Comp.1 Comp.2 Comp.3
## Standard deviation 25.0609944 2.297846646 1.952398023
## Proportion of Variance 0.9857302 0.008287118 0.005982713
## Cumulative Proportion 0.9857302 0.994017287 1.000000000