Sección 6 Estadística descriptiva
6.1 Funciones en R para calcular los estadísticos descriptivos
| Descripción | Función en R |
|---|---|
| Media | mean() |
| Varianza muestral | var() |
| Desviación estándar muestral | sd() |
| Mínimo | min() |
| Máximo | max() |
| Mediana | median() |
| Rango | range() |
| Quantiles | quantile() |
| Rango intercuantil | IQR() |
| Resumen | summary() |
| Moda | mfv()) del paquete statip o modeest |
Vamos a cargar la base de datos de iris y explorar estás funciones.
6.3 Medidas de variabilidad
- Mínimo:
## [1] 4.3- Máximo:
## [1] 7.9- Rango:
## [1] 4.3 7.9- Quantiles: La función en R para calcular cuantiles es
quantile(x, prob = seq(0,1,.25)), se puede especificar el vector de probabilidades con valores \([0,1]\) y el porcentaje, en el ejemplo se estan calculando los cuartiles ya que se especifico0.25. En el caso de querer los deciles se debería especificar0.1.
## 0% 25% 50% 75% 100%
## 4.3 5.1 5.8 6.4 7.9## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 4.30 4.80 5.00 5.27 5.60 5.80 6.10 6.30 6.52 6.90 7.90- Rango intercuantil:
## [1] 1.3- Varianza: La función en R
var()calcula la varianza muestral, es decir:
\[S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(x_i - \bar{x})^2\] Si lo que se quiere es la varianza muestral se puede realizar una función que realice esto.
## [1] 0.6856935## [1] 0.6811222Para muestras grandes la diferencia entre una y otra es pequeña pero para muestras pequeñas si es significativa la diferencia.
- Desviación estándar:
## [1] 0.8280661## [1] 0.82806616.4 Otras funciones
La función summary de R nos da un resumen de estas medidas de tendencia central y variabilidad, se puede usar tanto con una sola variable como con varias.
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 4.300 5.100 5.800 5.843 6.400 7.900## Sepal.Length Sepal.Width Petal.Length Petal.Width
## Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
## Median :5.800 Median :3.000 Median :4.350 Median :1.300
## Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
## Species
## setosa :50
## versicolor:50
## virginica :50
##
##
## Otra función que es útil en R es la función sapply(), esta nos permite calcular las medidas anteriores para cada columna de la base de datos.
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 5.843333 3.057333 3.758000 1.199333## Sepal.Length Sepal.Width Petal.Length Petal.Width
## 0% 4.3 2.0 1.00 0.1
## 25% 5.1 2.8 1.60 0.3
## 50% 5.8 3.0 4.35 1.3
## 75% 6.4 3.3 5.10 1.8
## 100% 7.9 4.4 6.90 2.5En el paquete pastecs se encuentra la función stat.desc() la cual nos regresa otras medidas.
## Sepal.Length Sepal.Width Petal.Length Petal.Width
## nbr.val 150.00 150.00 150.00 150.00
## nbr.null 0.00 0.00 0.00 0.00
## nbr.na 0.00 0.00 0.00 0.00
## min 4.30 2.00 1.00 0.10
## max 7.90 4.40 6.90 2.50
## range 3.60 2.40 5.90 2.40
## sum 876.50 458.60 563.70 179.90
## median 5.80 3.00 4.35 1.30
## mean 5.84 3.06 3.76 1.20
## SE.mean 0.07 0.04 0.14 0.06
## CI.mean.0.95 0.13 0.07 0.28 0.12
## var 0.69 0.19 3.12 0.58
## std.dev 0.83 0.44 1.77 0.76
## coef.var 0.14 0.14 0.47 0.64Esta función nos regresa el error estándar de la media (SE.mean), el intervalo de confianza para la media al p-valor de default 0.95 (CI.mean.95), el coeficiente de variación (coef.var) que es la desviación estándar entre la media.
En el caso de tener valores faltantes, algunas de las funciones de R regresan error o NA. El tratamiento a estos datos faltantes depende del tipo de valor faltante del que se trate:
MCAR: Missing completely at random, estos datos son cuando la probabilidad de pérdida no depende de lo observado ni de lo no observado, por ejemplo una muestra en un laboratorio accidentalmente se cae y se rompe, la letra del encuestador es ilegible.
MAR: Missing at random, en este caso el mecanismo de pérdida no depende de la información perdida pero si de la observada. Por ejemplo, en un estudio sobre los ingresos y pago de impuestos, las personas que ganan más se podrían negar a revelar sus ingresos. Si se conoce la categoría de pago de impuestos de todos los individuos, la no respuesta acerca del ingreso es MAR, el mecanismo de pérdida depende de la categoría de pago de impuestos(que si es observada), así que la pérdida del dato de ingreso NO depende del valor del ingreso mismo (que no se observo).
MNAR: Missing not at random, el mecanismo de pérdida no es ignorable si los valores perdidos dependen de los valores no observados. Por ejemplo, cuantas ayudas recibe la familia del gobierno, tienden a no contestar los que tienen más ayudas.
El tratamiento que se les debe dar a los datos depende de estas categorías, algunos de ellos son imputación simple, imputación múltiple, borrar casos, colocar la media en los valores faltantes, hot deck(se rellena con otro parecido), predicción, etc. En todos los casos uno puede sobreestimar los parámetros y nos puede llevar a tener resultados sesgados.
Si queremos digamos borrar los casos, en R especificamos na.rm= TRUE en las funciones.
## [1] 5.843333- Tablas de frecuencia
Vamos a cargar la base de datos HairEyeColor que contiene datos de sexo, color de cabello y ojos de 592 estudiantes.
datos <- as.data.frame(HairEyeColor)
hair_eye_color <- datos[rep(row.names(datos), datos$Freq), 1:3]
rownames(hair_eye_color) <- 1: nrow(hair_eye_color)
head(hair_eye_color)## Hair Eye Sex
## 1 Black Brown Male
## 2 Black Brown Male
## 3 Black Brown Male
## 4 Black Brown Male
## 5 Black Brown Male
## 6 Black Brown Male## hair_col
## Black Brown Red Blond
## 108 286 71 127## eye_col
## Brown Blue Hazel Green
## 220 215 93 64library(ggplot2)
df_hair <- as.data.frame(table(hair_col))
cl <- c("black", "brown", "red", "gold")
ggplot(df_hair, aes(x=hair_col, y= Freq, fill= hair_col)) +
geom_bar(stat = "identity")+
scale_fill_manual(values=cl)+
labs(title = "Color de cabello de 592 estudiantes",
subtitle = "HairEyeCol data set",
x = "Color de cabello",
y = "Cantidad de estudiantes",
caption = "Datos: data(HairEyeCol)`",
fill = "Color de Cabello")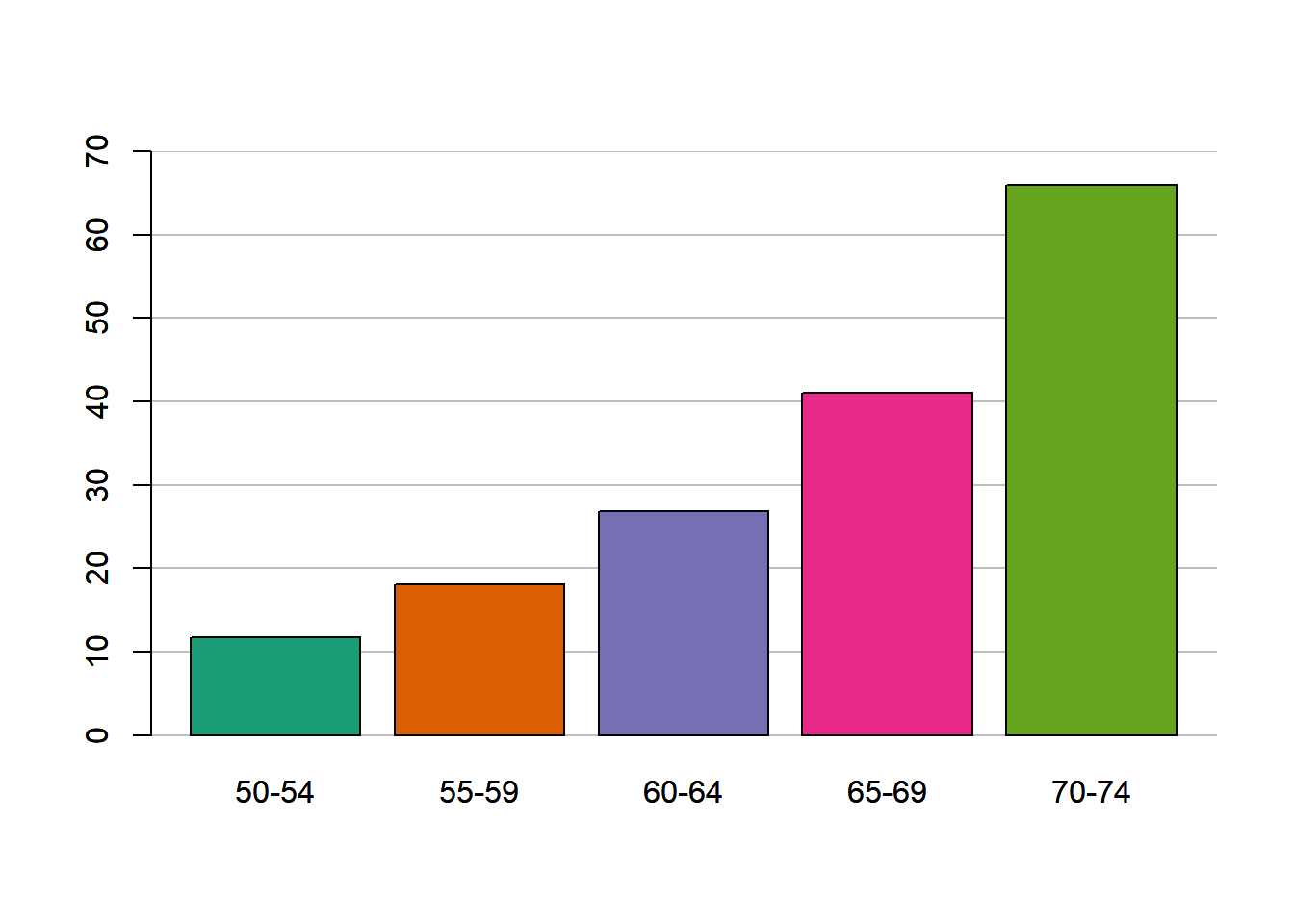
- Tabla de contingencia para dos variables:
## eye_col
## hair_col Brown Blue Hazel Green
## Black 68 20 15 5
## Brown 119 84 54 29
## Red 26 17 14 14
## Blond 7 94 10 16df_hair_eye <- as.data.frame(datos2)
p <- ggplot(df_hair_eye, aes(x=hair_col, y= Freq, fill=eye_col)) +
geom_bar(stat = "identity") +
labs(title = "Color de cabello de 592 estudiantes",
subtitle = "HairEyeCol data set",
x = "Color de cabello",
y = "Cantidad de estudiantes",
caption = "Datos: data(HairEyeCol)`",
fill = "Color de Cabello")
p + scale_fill_manual(values = c("brown","blue", "gold", "green"))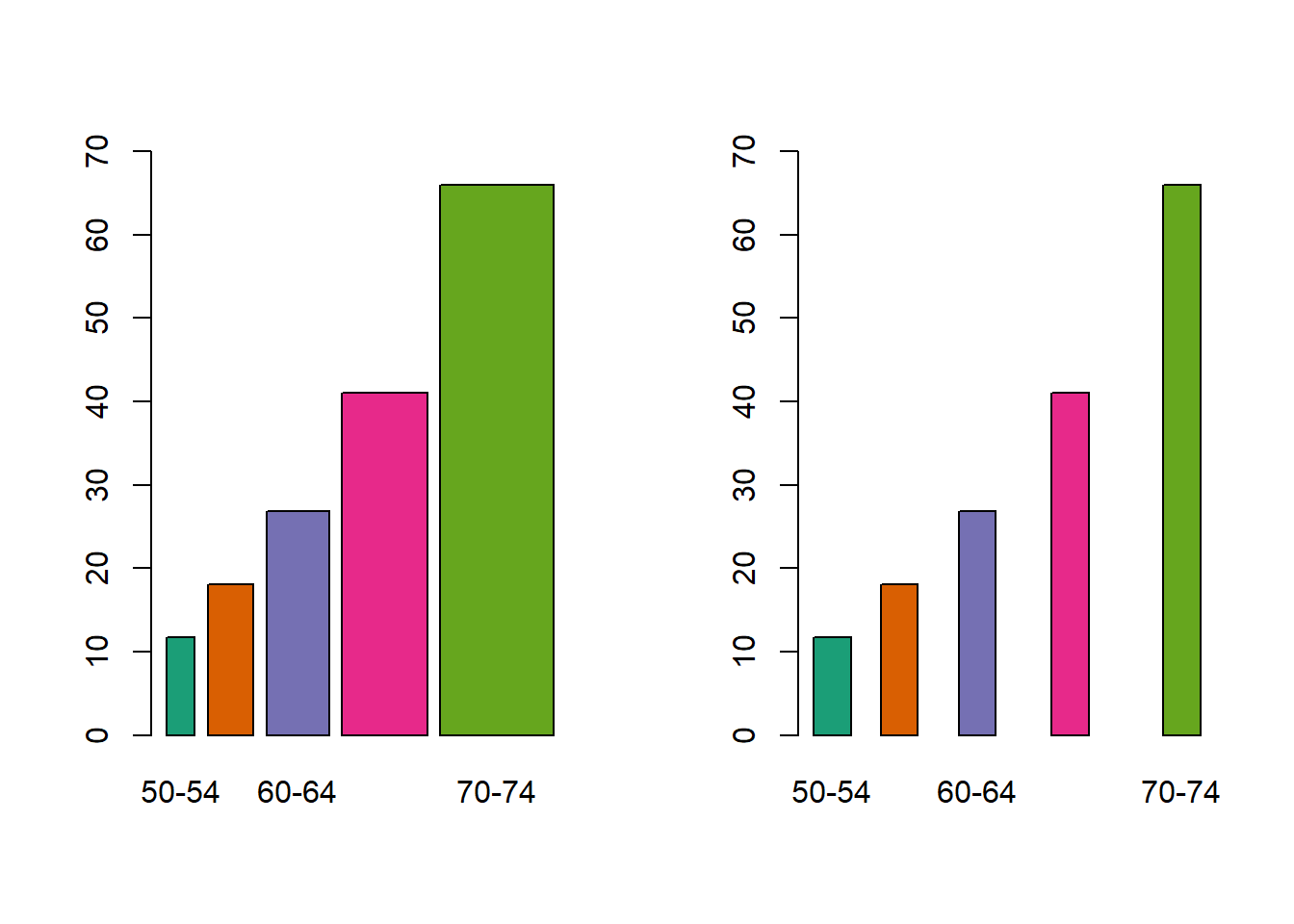
p2 <- ggplot(df_hair_eye, aes(x=hair_col, y= Freq, fill=eye_col)) +
geom_bar(stat = "identity", position = position_dodge()) +
labs(title = "Color de cabello de 592 estudiantes",
subtitle = "HairEyeCol data set",
x = "Color de cabello",
y = "Cantidad de estudiantes",
caption = "Datos: data(HairEyeCol)`",
fill = "Color de Cabello")
p2 + scale_fill_manual(values = c("brown","blue", "gold", "green"))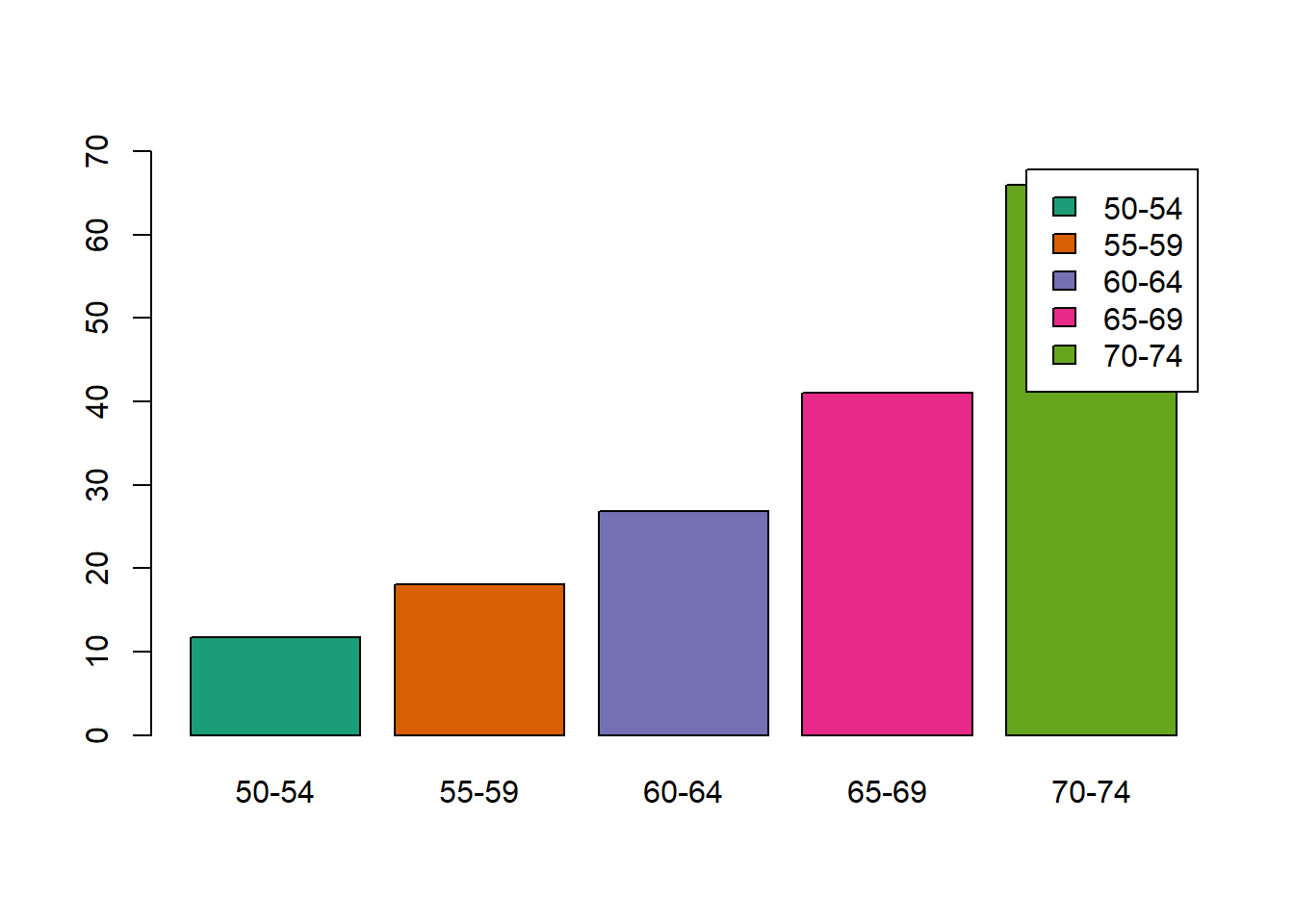
6.5 Ejercicios
- Analiza la Tabla siguiente (Consumer Report Buying Guide 2002) que contiene algunos datos (precio, calidad de sonido, caseteras, etc.) de algunas marcas de minicomponentes y responde las siguientes preguntas:
| Marca y modelo | Precio \((\$)\) | Calidad de sonido | Capacidad para CD | Sintonización FM | Caseteras |
|---|---|---|---|---|---|
| Aiwa NSX-AJ800 | 250 | Buena | 3 | Regular | 2 |
| JVC FS-SD1000 | 500 | Buena | 1 | Muy buena | 0 |
| JVC MX-G50 | 200 | Muy buena | 3 | Excelente | 2 |
| Panasonic SC-PM11 | 170 | Regular | 5 | Muy buena | 1 |
| RCA RS 1283 | 170 | Buena | 3 | Mala | 0 |
| Sharp CD-BA2600 | 150 | Buena | 3 | Buena | 2 |
| Sony CHC-CL1 | 300 | Muy buena | 3 | Muy buena | 1 |
| Sony MHC-NX1 | 500 | Buena | 5 | Excelente | 2 |
| Yamaha GX-505 | 400 | Muy buena | 3 | Excelente | 1 |
| Yamaha MCR-E100 | 500 | Muy buena | 1 | Excelente | 0 |
- ¿Cuántos elementos contiene este conjunto de datos y cuál es la población?
- Calcula el precio promedio en la muestra.
- Con el resultado anterior, estima el precio promedio para la población.
- ¿Cuántas variables hay en este conjunto de datos? Clasifícalas en cuantitativas y cualitativas
- ¿Qué porcentaje de los minicomponentes tienen una sintonización de FM buena o excelente?
- Un biólogo que estudia cierta reserva ecológica está interesado en analizar su temperatura. A continuación se presenta las temperaturas promedio observadas de 40 días elegidos aleatoriamente.
Temperaturas observadas (en °C)
14.4, 17.5, 31.1, 28.0, 17.2, 34.1, 21.8, 18.1, 19.0, 25.0, 21.1, 27.8, 28.7, 21.1, 26.1, 33.6, 29.0, 20.2, 31.3, 25.1,31.6, 25.2, 19.0, 26.3, 25.5, 16.9, 20.9, 23.2, 26.6, 32.0, 28.2, 22.3, 29.2, 22.6, 29.6, 16.6, 22.7, 23.9, 26.3, 24.6
- Construye la distribución de frecuencias individuales y acumuladas (absolutas y relativas) de la temperatura de la reserva ecológica considerando 5 clases de igual longitud sobre el intervalo [10, 40].
- Construye el histograma de frecuencias relativas de la temperatura de la reserva ecológica considerando las clases del inciso anterior.
- Construye la ojiva de la temperatura de la reserva ecológica considerando las clases del inciso 1. Consultar liga para la realización de la ojiva.
- Calcula la media, mediana y moda de los datos.
- A continuación se presenta el diagrama de tallo y hojas del contenido de cloro (en mililitros) de una muestra de 20 botes de un lote de producción.
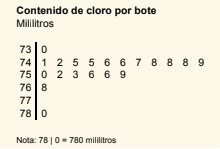
Figure 6.1: Contenido de cloro
- Calcula el percentil 0.05 de la distribución del contenido de cloro por bote.
- Calcula el cuantil 0.05 de la distribución del contenido de cloro por bote.
- Calcula los cuartiles de la distribución del contenido de cloro por bote.
- Calcula los coeficientes de asimetría y curtosis.
Nota: El coeficiente de asimetría mide la proximidad de los datos a su media. Cuando mayor sea la suma \(\sum_{i=1}^n(x_i - \bar{x})^3\) mayor será la asimetría. Para una colección de datos \(x_1,x_2,...,x_n\) con media \(\bar{x}\) y desviación estándar \(s\), el coeficiente de asimetría se calcula como:
\[k=\frac{1}{s^3}\left( \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})^3\right)\]
La curtosis mide que tan puntiaguda o achatada es la distribución de los datos, indica la cantidad de datos que hay cercanos a la media, para una colección de datos \(x_1,x_2,...,x_n\) con media \(\bar{x}\) y desviación estándar \(s\) esta dado por el número: \[k=\frac{1}{s^4}\left( \frac{1}{n}\sum_{i=1}^n(x_i - \bar{x})^4\right)\]
- Los siguientes tiempos (cronometrados en segundos) fueron registrados por una muestra de 5 corredores durante una carrera de 100 metros planos: 9.82, 9.91, 9.94, 9.95 y 9.98.
- Calcula la amplitud o rango de los tiempos observados.
- Calcula la varianza de los tiempos observados.
- Calcula la desviación estándar de los tiempos observados.
- Calcula el coeficiente de variación de los tiempos observados. Interprete.
- La Figura siguiente muestra una tabla que contiene el número de accidentes de tráfico en una muestra de estados (de Estados Unidos), entre 2007 y 2008. Grafica un scatter plot y encuentra el coeficiente de correlación muestral para los pares de datos.
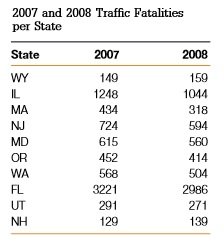
Figure 6.2: Datos de Accidentes de Tráfico
- En cada uno de los siguientes casos determina qué tipo de escala de medición es la más adecuada para cada una de ellas:
- El Director de Mercadotecnia de una Editorial desea conocer la opinión del público respecto a las secciones (política, finanzas, deportes, cultura, ciudad,cocina) que debe incluir una nueva revista.
- El Gobierno de la Ciudad de México desea conocer si los habitantes del Distrito Federal están a favor o en contra de la construcción de un nuevo distribuidor vial.
- Con la finalidad de establecer estándares de calidad, una cadena de restaurantes desea conocer la calificación (excelente, bueno, regular, malo) que dan sus clientes a los meseros.
- El Director de Operaciones de Teléfonos de México (TELMEX), desea conocer el número de llamadas de larga distancia que se realizan por mes.
- La Comisión Nacional de Aguas quiere estimar el consumo promedio de agua por familia en cada uno de los municipios del Estado de México.
- Un Biólogo desea determinar la temperatura que debe tener un estanque para tener cierta especie de ballenas en cautiverio.